基于回归分析的波士顿房价分析
基于回归分析的波士顿房价分析
项目实现步骤:
1.项目结构
2.处理数据
3.处理绘图
4.对数据进行分析
5.结果展示
一.项目结构

二.处理数据
from sklearn import datasets
import pandas as pd
"""
sklearn1.2版本后不在保留load_boston数据集,
可用
"""
def get_data():
# 获取波士顿数据
# data_url = "http://lib.stat.cmu.edu/datasets/boston"
# raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
# print(raw_df)
# # 输入
# boston_x = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
# # 输出
# boston_y= raw_df.values[1::2, 2]
# # 自作数据集
# boston=pd.DataFrame(boston_x)
# print(boston)
boston=datasets.load_boston()
# 输入
boston_x=boston.data
# 输出
boston_y=boston.target
# 自制数据集
boston_new=pd.DataFrame(boston_x)
boston_new.columns=boston["feature_names"]
boston_new['PRICE']=boston_y
# 保存数据
# boston_new.to_csv('./models/Data/boston.csv')
return boston_new
使用sklearn的datasets时,对应的波士顿房价数据已经被“移除”,在获取数据时,会出现

,此时,在该提示的下方会有相关的解决方法

不建议使用提供的方法,对应方法的数据与具体实现项目的数据有误差
三.处理绘图
1.绘图前准备
import numpy as np
def get_request(request,data):
# 要处理的数据
# 设置初始值
control={
'CRIM':'城镇人均犯罪率',
'ZN':'占地面接超过5万平方米英尺的住宅用地面积',
'INDUS':'城镇非零售业务的比例',
'CHAS':'查尔斯河虚拟变量',
'NOX':'一氧化碳浓度',
'RM':'平均每个居民拥有的房数',
'AGE':'在1940年前建成的所有者占用单位的比例',
'DIS':'与五个波士顿就业中心的加权距离',
'TAX':'每10000美元的全额物业说率',
'PTRATIO':'城镇师生比',
'B':'城镇黑人比例',
'LSTAT':'低收入人口所占比例',
'PRICE':'房价'
}
if request in control.keys():
# 获取价格的最大值和最小值
max=np.max(data['PRICE'])
min=np.min(data['PRICE'])
# 存储最大值和最小值,对应的x轴标签,y轴的标签
request_data=list((max,min,control[request],control['PRICE']))
return request_data
else:
print('你输入的数据不存在,请查看相关的文档,查看你想要的数据类型')
用于处理绘图前的准备工作,获取对应的数据和标签
绘图
import matplotlib
import matplotlib.pyplot as plt
from models.chart.beforedraw import beforedraw
from models.CleanData.resolvedata import resolve_data
# 画图类
class draw:
def __init__(self,request):
self.data=resolve_data.get_data()
matplotlib.rc('font',family='SimHei')
plt.rcParams['axes.unicode_minus']=False
before_draw=beforedraw.get_request(request,self.data)
self.x_ticks_max=before_draw[0]
self.x_ticks_min=before_draw[1]
self.x_label=before_draw[2]
self.y_label=before_draw[3]
self.request=request
def draw_sactter(self):
plt.scatter(self.data['PRICE'],self.data[self.request])
plt.title(f'{self.x_label}与{self.y_label}的散点图')
plt.xlabel(self.x_label)
plt.ylabel(self.y_label)
plt.xticks((range(int(self.x_ticks_min),int(self.x_ticks_max),10)))
plt.grid()
plt.show()
def draw_polt(self,title,x_data,y_data,x_label=None,y_label=None):
plt.plot(x_data,y_data)
plt.title(title)
plt.xlabel(x_label)
plt.ylabel(y_label)
plt.show()
def draw_bar(self,title,x_data,y_data,x_label=None,y_label=None):
plt.bar(x_data,y_data)
plt.title(title)
plt.xlabel(x_label)
plt.ylabel(y_label)
plt.show()
将绘图封装成类,便于后期的绘图
四.对数据进行分析
分别实现房价与各参数的线性回归分析,绘制出房价的预测值;蚕蛹逻辑回归分析,对是否居住在河边进行逻辑回归分析
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from sklearn.model_selection import train_test_split
from models.CleanData.resolvedata import resolve_data
from models.chart.draw import draw
from sklearn.preprocessing import StandardScaler
from sklearn.impute import SimpleImputer
from sklearn.linear_model import LinearRegression
# 回归/分类模型的评价方法
from sklearn.metrics import mean_squared_error #MSE
from sklearn.metrics import mean_absolute_error #MAE
# 分类
from sklearn.linear_model import LogisticRegression
class Learning():
def __init__(self):
self.data=resolve_data.get_data()
self.values=self.data.values
self.columns=self.data.columns
self.x_train = ''
self.x_test = ''
self.y_train = ''
self.y_test = ''
self.train_test_split_linear()
self.draw=draw.draw("ZN")
self.fill_nan()
self.log()
# 切分数据集
def train_test_split_linear(self):
self.x_train,self.x_test,self.y_train,self.y_test=train_test_split(self.values[:,0:-1],self.values[:,-1],test_size=0.2)
# 弥补缺失值
def fill_nan(self,):
if sum(self.data.isnull().sum())!=0:
simple_imp=SimpleImputer(missing_values=np.nan,strategy='mean')
self.data=simple_imp.fit(self.data)
self.standard_scaler()
# 归一化
def standard_scaler(self):
scaler=StandardScaler()
# fit_transform()一般用于训练集,transform一般用于测试集
self.x_train=scaler.fit_transform(self.x_train)
self.x_test=scaler.transform(self.x_test)
self.linear()
# 线性回归
def linear(self):
linear=LinearRegression()
self.models_1=linear.fit(self.x_train,self.y_train)
# 对模型进行打分
# print(self.models.score(self.x_test,self.y_test))
self.linear_metrics()
def linear_metrics(self):
# MSE均方误差
linear_MSE=mean_squared_error(self.y_train,self.models_1.predict(self.x_train))
# RMSE均方根误差 MSE的开方
linear_RMSE=mean_squared_error(self.y_train,self.models_1.predict(self.x_train))**0.5
# MAE平均绝对误差
linear_MAE=mean_absolute_error(self.y_train,self.models_1.predict(self.x_train))
# 误差
print(f'MSE均方误差:{linear_MSE},RMSE均方根误差{linear_RMSE},MAE平均绝对误差{linear_MAE}')
# 房价预测值
self.draw.draw_polt("房价预测值",np.linspace(0,100,102),self.models_1.predict(self.x_test))
# 分类
def log(self):
# 测试集
x_log_l=self.values[:,0:1]
x_log_r=self.values[:,4:]
y_log=self.values[:,3]
x_log=np.hstack((x_log_l,x_log_r))
log=LogisticRegression()
x_train,x_test,y_train,y_test=train_test_split(x_log,y_log,test_size=0.3)
models_2=log.fit(x_train,y_train)
# 预测值
print(x_test,models_2.predict(x_test))
# 评分
print(models_2.score(x_test,y_test))
# 权重
print(models_2.coef_)
self.draw.draw_polt("权重图",np.linspace(0.1,0.9,11),models_2.coef_[0],'','')
one_array=[]
zero_array=[]
for item in models_2.predict(x_test):
if item==0:
zero_array.append(item)
else:
one_array.append(item)
self.draw.draw_bar("预测值计较",['0','1'],[len(zero_array),len(one_array)])
五.结构展示
线性回归的误差分析结果

线性回归的房价预测
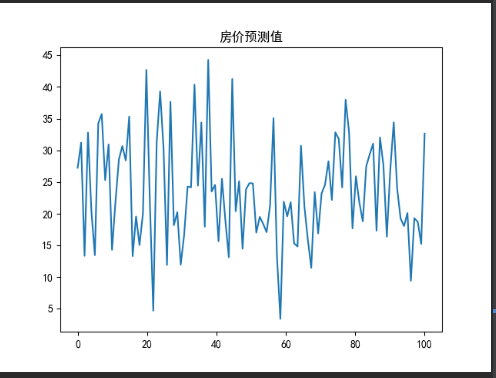
逻辑回归的权重图

逻辑回归的预测图

在逻辑回归中,各阐述对于是否居住于河边的影响大,对应的评分在80%以上
项目完成!!!