在科学计算领域独领风骚，NumPy书写辉煌传奇

在数字世界的边缘，有一座神奇的城市，这座城市由无数个数据点和向量构成，街道上流淌着数不清的数组和矩阵。在城市的中心，耸立着一座巨大的科学计算塔，它的外墙是由数学符号和代码构成，散发着闪烁的数字光芒。城里的居民们穿梭于数组的巷道间，驾驭着向量的飞船，探索着数据的深海，寻找着数学的奥秘。这里，每一个函数、每一个对象，都是城市的一部分，编织成了一张无比庞大的数学网络。

这里不仅是科学计算的殿堂，更是数学与编程的交汇之地，这个就是今天的主角NumPy。

NumPy是什么

NumPy是Numerical Python的缩写，有人读作兰派，也有人读作兰皮，他是Python中一个重要的科学计算库，是一个非常流行的Python第三方库，关于Python第三方库，可以看这里，《Python第三库介绍》。

NumPy就是用来科学计算的，不要听科学两个字给吓到了，实际上也没有太高深，主要是用于处理和操作大型多维数组以及进行数值计算。它提供了高效的数组对象和各种操作数组的函数，是很多其他科学计算库和数据分析库的基础。

NumPy的核心是多维数组对象（称为ndarray），它可以容纳各种数据类型（如整数、浮点数、布尔值等）的元素，并且可以通过整数索引快速访问和操作数组中的数据。NumPy提供了许多用于创建、操作和处理数组的函数和方法，如矩阵运算、数学函数、逻辑运算、排序和统计分析等。

安装NumPy

当你开始使用NumPy时，首先需要安装NumPy库。可以使用以下命令通过pip安装NumPy：

pip install numpy

安装完成后，就可以在你的Python代码中导入NumPy库并开始使用。

使用NumPy

安装完成后，在 Python 脚本中引入 NumPy 模块，这里需要注意的是，我们平时正式中把NumPy写成大小写的形式，但是在使用的时候都是要小写的，否则会提示找不到相应的模块。

import numpy

不可以这样

import NumPy

用NumPy进行数组操作

下面是一个使用NumPy的简单示例，以创建一个一维数组并进行一些常见的操作为例：

import numpy as np

# 创建一维数组
arr = np.array([1, 2, 3, 4, 5])
print(arr)  # 输出：[1 2 3 4 5]

# 访问数组元素
print(arr[0])  # 输出：1
print(arr[2:4])  # 输出：[3 4]

# 数组运算
print(arr + 2)  # 输出：[3 4 5 6 7]
print(arr * 2)  # 输出：[ 2  4  6  8 10]
print(np.sqrt(arr))  # 输出：[1.         1.41421356 1.73205081 2.         2.23606798]

# 数组形状修改
arr_reshape = arr.reshape((5, 1))
print(arr_reshape)
# 输出：
# [[1]
#  [2]
#  [3]
#  [4]
#  [5]]

# 数组统计
print(np.mean(arr))  # 输出：3.0
print(np.max(arr))  # 输出：5
print(np.sum(arr))  # 输出：15

# 数组操作
arr2 = np.array([6, 7, 8, 9, 10])
print(np.concatenate((arr, arr2)))  # 输出：[ 1  2  3  4  5  6  7  8  9 10]

以上是一些使用NumPy的基本操作示例，通过NumPy提供的各种函数和方法，你可以进行更复的数组操作、数值运算、统计分析等，这个主要就是NumPy的一些比较小的功能，Numpy的强大功能肯定不止于此。

用Numpy解方程

假设有如下线性方程组：

2x + y = 5
x - 3y = -1

我们可以将系数矩阵和常数项向量表示成NumPy数组，然后使用numpy.linalg.solve()函数求解方程组。

import numpy as np

# 定义系数矩阵，就是方程组左边x，y前面的系数
a = np.array([[2, 1], [1, -3]])

# 定义常数项向量，就是方程组右边的数值
b = np.array([5, -1])

# 求解方程组
x = np.linalg.solve(a, b)

print("方程组的解为：", x)

运行结果后输出：

方程组的解为： [[2.]
 [1.]]

说明方程组的解就是x=2, y=1，这样就很好的求出了二元一次方程组的答案，这就是把数学问题用代码的形式表现出来。当然，Numpy肯定也是可以处理更加复杂的方程组计算，大家可以去了解相关的文档。

NumPy在机器学习中的应用

在机器学习领域中，NumPy常常用于数据的预处理和特征工程阶段。

在许多机器学习算法中，特征缩放是一个重要的步骤，目的是将数据特征进行归一化处理，使得不同特征之间具有相似的数值范围，从而提高算法的性能和收敛速度。

假设我们有一个数据集，其中包含两个特征：年龄和收入。年龄的取值范围是0到100，收入的取值范围是1000到100000。我们希望将这两个特征进行缩放，使得它们的取值范围都在0到1之间。

import numpy as np

# 原始数据
age = np.array([20, 40, 60, 80])
income = np.array([1000, 5000, 20000, 80000])

# 特征缩放
age_scaled = (age - np.min(age)) / (np.max(age) - np.min(age))
income_scaled = (income - np.min(income)) / (np.max(income) - np.min(income))

# 打印缩放后的结果
print("缩放后的年龄：", age_scaled)
print("缩放后的收入：", income_scaled)

运行上述代码，将得到以下输出结果：

缩放后的年龄： [0.         0.33333333 0.66666667 1.        ]
缩放后的收入： [0.         0.05063291 0.24050633 1.        ]

可以看到，经过特征缩放后，年龄的取值范围变为0到1之间，收入也变为0到1之间，使得数据在同一数值范围内，方便后续的机器学习算法处理。当然关于机器学习，更专业的库的是Tesnsorflow，只是底层都是基于NumPy构建的。

NumPy在物理建模中的应用

有时候，在现实世界中的一些物理规律，我们需要通过有规则的线条来表示出来，那么就也需要用到NumPy这个库了，比如我们需要知道摆锤的运动过程，随时间变化的过程中摆角一些变化规律。

import numpy as np
import matplotlib.pyplot as plt

# 定义常数
g = 9.81  # 重力加速度 m/s^2
L = 1.0   # 摆长 m
dt = 0.01 # 时间步长 s
T = 10    # 总时间 s

# 初始化数组
N = int(T/dt)
theta = np.zeros(N)
omega = np.zeros(N)

# 设置初始条件
theta[0] = np.pi/4  # 初始偏转角度 45度
omega[0] = 0        # 初始角速度

# 数值求解
for i in range(N-1):
    omega[i+1] = omega[i] - (g/L) * np.sin(theta[i]) * dt
    theta[i+1] = theta[i] + omega[i+1] * dt

# 绘制摆锤运动角度随时间变化图
t = np.arange(0, T, dt)
plt.plot(t, theta)
plt.xlabel('Time (s)') #时间
plt.ylabel('Pendulum angle (in radians)') #摆角 (弧度)
plt.title('Pendulum motion simulation') #摆锤运动模拟
plt.grid()
plt.show()

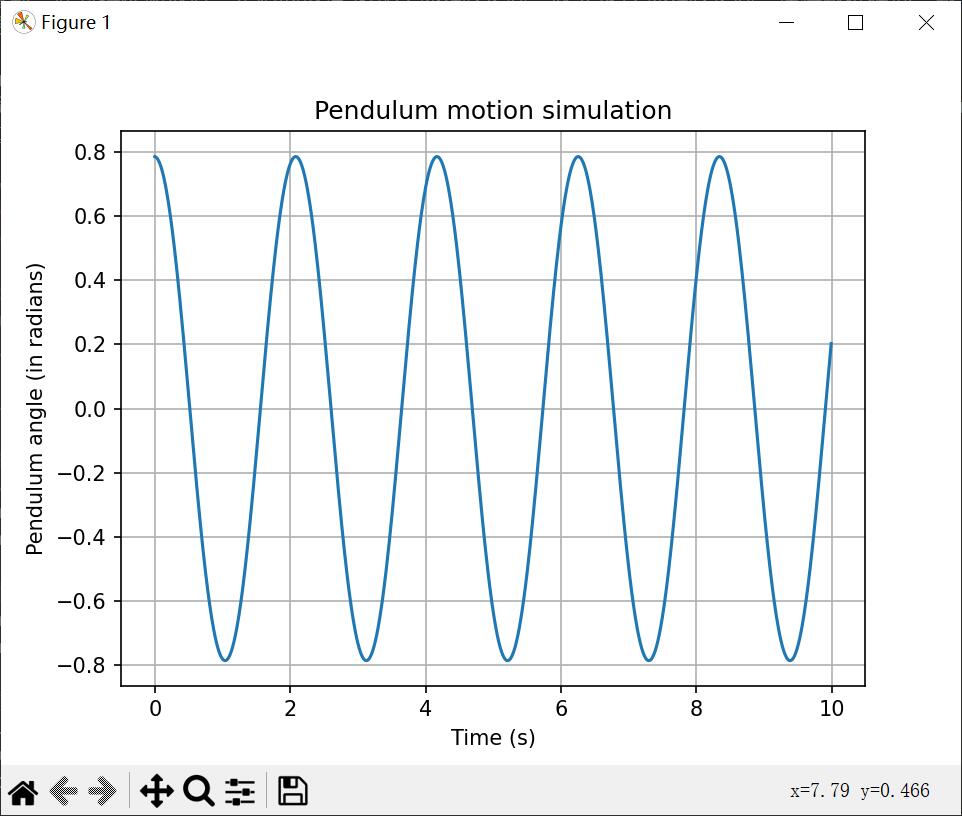
以上这段代码是一个简单的模拟摆锤（简谐摆）运动的过程，通过数值求解来模拟摆锤在重力场中的运动。这里NumPy的主要作用就是初始化了两个数组theta 和omega，分别用于存储摆锤的角度和角速度。当然需要用到matplotlib这个第三库，来输出摆锤的运动轨迹。以下是这个程序的输出：

NumPy社区

目前NumPy是托管在github上面的，从github上面的star数量可以看出，这个库还是非常受欢迎的。目前主要Python和C/C++来开发的，开发者如果对这个第三库有兴趣，可以自行提交相关的补丁。

更多精彩内容，请关注同名公众：一点sir（alittle-sir）

热门相关：傲天弃少   豪门退婚妻：宝贝，再嫁我一次！   异界之极品奶爸   一级BOSS：你结婚，我劫婚   驭房之术