OCR 文字检测(Differentiable Binarization --- DB)
文本检测

基于分割的做法(如蓝色箭头所示):
传统的pipeline使用固定的阈值对于分割后的热力图进行二值化处理
- 首先,它们设置了固定的阈值,用于将分割网络生成的概率图转换为二进制图像
- 然后,用一些启发式技术(例如像素聚类)用于将像素分组为文本实例
DB的做法(如红色箭头所示):
而本文提出的pipeline会将二值化操作嵌入到分割网络中进行组合优化,会生成与热力图对应的阈值图,通过二者的结合生成最终的二值化操作。
- 在得到 分割map后,与网络生成的threshold map一次联合做可微分二值化得到二值化图,然后再经过后处理得到最终结果。
- 将二值化操作插入到分段网络中以进行联合优化,通过这种方式,可以自适应地预测图像每个位置的阈值,从而可以将像素与前景和背景完全区分开。 但是,标准二值化函数是不可微分的,因此,我们提出了一种二值化的近似函数,称为可微分二值化(DB),当训练时,该函数完全可微分。将一个固定的阈值训练为一个可学习的每个位置的阈值
标签生成
首先看label是如何生成的,网络要学习的目标gt 与 threshold map是怎样的生成和指导网络去训练的,知道threshold_map的label值跟gt的值,我们才能更好地去理解“可微分二值化”是如何实现的;

给定一张文字图像,其文本区域的每个多边形由一组线段描述:
\(\ G = \{s_k\}^n_{k = 1}\)
其中,n表示顶点的数量
使用Vatti clipping algorithm (Vati 1992)缩小多边形,对 gt 多边形(polygon) 进行缩放;收缩偏移量(offset of shrinking)\(D\) 可以通过周长 \(L\) 和面积 \(A\) 计算:
\(\ D = \frac {A(1-r^2)}{L}\)
其中,\(r\) 是缩放比例,依经验一般取值为 0.4
- 这样我们就通过 gt polygon 形成 缩小版的 polygon 的gt mask图 probability map(蓝色边界)
- 以同样的 offset D 从多边形polygon \(G\) 拓展到 \(G_d\) ,得到如图中 threshold_map中的(绿色边界)
threshold_map中由 \(G_s\) 到 \(G_d\) 之间形成了一个文字区域的边界。
一组图来可视化图像生成的结果:

我们可以看到 probability map 的 gt 是一个完全的0,1 mask ,polygon 的缩小区域为1,其他背景区域为0;
但是在threshold_map文字边框值并非0,1;
使用PyCharm的view array 我们能看到threshold_map中文字边框的数值信息:

文字最外圈边缘为0.7,靠近中心区域是为0.3的值。(0.3-0.7为预设的阈值最大最小值)。我们可以看到文字边界为阈值最大,然后根据文字实例边缘距离逐渐递减。
知道threshold_map的label值跟gt的值,我们才能更好地去理解“可微分二值化”是如何实现的;
获取边界框

整体流程如图所示:
- backbone网络提取图像特征
- 类似FPN网络结构进行图像特征融合后得到两个特征图 probability map 跟 threshold map
- probability map 与threshold map 两个特征图做DB差分操作得到文字区域二分图
- 二分图经过cv2 轮廓得到文字区域信息
首先,图片通过特征金字塔结构的backbone,通过上采样的方式将特征金字塔的输出变换为同一尺寸,并级联(cascade)产生特征F;然后,通过特征图F预测概率图(P — probability_map)和阈值图(T — threshold_map); 最后,通过概率图P和阈值图T生成近似的二值图(B — approximate_binary_map)。
在训练阶段,监督被应用在阈值图、概率图和近似的二值图上,其中后两者共享同一个监督;在推理阶段,则可以从后两者轻松获取边界框。
可微的二值化(Differentiable binarization)
传统的阈值分割做法为:

$\ B_{i,j} $ 代表了probability_map中第i行第j列的概率值。这样的做法是硬性将概率大于某个固定阈值的像素作为文字像素,而不能将阈值作为一个可学习的参数对象(因为阈值分割没办法微分进行梯度回传)
可微分的二值化公式:

首先,该公式借鉴了sigmod函数的形式(sigmod 函数本身就是将输入映射到0~1之间),所以将概率值 $\ P_{i,j} $ 与阈值 $\ T_{i,j} $ 之间的差值作为sigmod函数的输出,然后再经过放大系数 \(k\), 将其输出无限逼近两个极端 0 或者1;其中,k为放大因子,依经验设定为 50
带有自适应阈值的可微分二值化不仅有助于把文字区域与背景区分开,而且还能把相近的实例分离开来。

我们来根据label generation中的gt 与 threshold_map来分别计算下。经过这个可微分二值化的sigmod函数后,各个区域的像素值会变成什么样子:
文字实例中心区域像素:
- probability map 的gt为 1
- threshold map的gt值为0.3

如果不经过放大系数K的放大,那么区域正中心的像素如上图所示经过sigmod函数后趋向于0.6左右的值。但是经过放大系数k后,会往右倾向于1。
文字实例边缘区域像素:
- probability map 的gt为 1
- threshold map的gt值为0.7

如果不经过放大系数K的放大,那么区域正中心的像素如上图所示经过sigmod函数后趋向于0.5左右的值。但是经过放大系数k后,会往右倾向于1。
文字实例外的像素:
- probability map 的gt为 0
- threshold map的gt值为0.3

经过放大系数k后,激活值会无限趋近于0; 从而实现二值化效果。
解释了DB利用类似sigmod的函数是如何实现二值化的效果,那么我们来看其梯度的学习性:
传统二值化是一个分段函数,如下图所示:
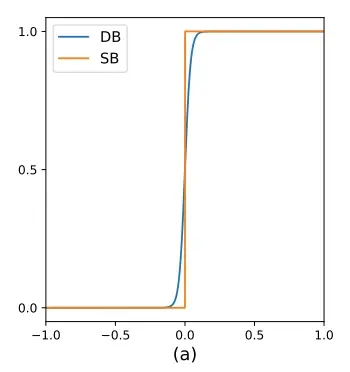
SB:standard binarization其梯度在0值被截断无法进行有效地回传。 DB:differentiable binarization是一个可微分的曲线,可以利用训练数据+优化器的形式进行数据驱动的学习优化。
我们来看其导数公式,假设 \(l_+\) 代表了正样本, \(l_-\) 代表了负样本,则:

根据链式法则我们可以计算其loss梯度
百度paddle中提供的接口可以实现下面的效果:
