【翻译】为什么我们需要极限和无穷小?(Why Do We Need Limits and Infinitesimals?)
那么多数学课,没有任何上下文,就跳到极限,无穷小,非常小的数(T)。但是我们为什么要在乎呢?数学帮助我们模拟世界。我们可以把一个复杂的想法(一条蜿蜒的曲线)分解成更简单的部分(矩形):

但是,我们想要一个精确的模型。矩形越细,模型越精确。从矩形构建的更简单的模型比直接处理复杂的无定形斑点更容易分析。棘手的部分是制作一个像样的模型。极限和无穷小有助于我们创建简单易用的模型,但与原始项目具有相同的属性(长度、面积等)。
零的悖论
将一条曲线分割成矩形有一个问题:我们如何让切片薄到我们注意不到它们,但大到足以“存在”?
如果切片太小而不能被注意到(零宽度),那么模型看起来与原始形状相同(我们看不到任何矩形!).现在没有任何好处了一一“简单”模型和原始模型一样复杂!此外,将零宽度切片相加不会让我们有任何进展。
如果切片很小但可以测量,幻觉就消失了。我们看到,我们的模型是一个锯齿状的近似,不会是准确的。数学家能做什么?我们希望两者兼得:切片薄到我们看不到它们(对于一个精确的模型),切片厚到足以创建一个更简单、更容易分析的模型。进退两难!
解决方法:零是相对的
零的概念被我们的期望所误导。“0+i”这个纯虚数和零一样吗?
当我们在实数线上时,“I”看起来肯定是零:I的“实部”R(i)确实是0。
一个纯虚数还能去哪里?(正北向东多远?)
这里有一个不同的脑筋急转弯:在读这句话的时候,你的体重有没有零磅的变化?是的,以你附近的任何规模。但是原子测量将显示由于汗液蒸发、呼气等引起的一些质量变化。
你看,有两个答案(目前为止!)到“是零和不是零”的悖论:
- 允许另一个维度:在我们的维度中测量为零的数字可能实际上很小,但在另一个维度中不为零(无限小方法一一一个比我们处理的维度小无限多的维度)
接受不完美:被测量为零的数字在更高的精确度下可能是非零的;说某物是“零”实际上意味着“它是0”+/-我们的测量误差”(极限逼近)这些方法弥合了“对我们来说为零”和“在更高精度水平上非零”之间的差距。
极限和无穷小概述
让我们看看每种方法是如何将曲线分割成矩形的:
- 极限:“给我你的误差范围(我知道你有,你这个有限的,不完美的人类!),我给你画条曲线。
你的尺子上最小的单位是什么?英寸?好吧,我给你画一个毫米级的staircasey曲线,你永远也不会知道。哦,你有一把毫米尺,是吗?我用纳米来画曲线。不管你的准确性如何,我更好。你永远不会看到楼梯。” - 无穷小:“忘记准确性:有一个完整的极限空间,我将在那里画曲线。
精度完全不是你能达到的一一我是亚原子水平,你是个几乎不能走路和嚼口香糖的穴居人。这就像从真实的平面到达想象的平面一一你就是做不到。对你来说,我在亚原子水平上制作的矩形是你见过的最完美的曲线。”极限存在于我们的维度中,但其精确度足以维持完美模型的幻觉。无穷小在另一个维度建立模型,在我们的维度看起来完全准确。这两种方法的诀窍在于,更简单的模型超出了我们的精度水平。我们可能知道这个模型是锯齿状的,但我们无法区分一我们做的任何测试都显示模型和实物是一样的。那一招不管用吧?
哦,但确实如此。我们总是被“不完美但有用”的模型所欺骗:
- 音频文件不包含原始信号的所有信息。但是你能说出一个高质量的mp3和一个人在另一个房间里说话的区别吗?
- 计算机打印输出是由小到看不见的单个点组成的。你能把手写的笔记和高质量打印的笔记区分开来吗?
- 视频以每秒24次的速度显示静止图像。这个“不完美”的模型快到足以欺骗我们的大脑看到流体运动。
如此循环往复。我们抵制是因为我们对精确性的人为需求。但是音频和视频工程师知道他们不需要一个完美的复制品,只要质量好到足以欺骗我们认为这是原件。微积分让我们制造出这些技术上不完美但“足够精确”的数学模型。在另一个维度工作在用简化模型进行推理时,我们需要小心。我们需要在更高的精确度水平上“做我们的工作”,并将nnI结果带回我们的世界。否则我们会丢失信息。
假设一个虚数(I)访问实数线。大家都觉得他是零:毕竟Re(1)=0。但是我会变戏法!“帮我摆平!”他说,他们也这么做了:“ii=-1”其他的数字都很惊讶。对于实数,似乎出现了“0’0=-1”这一巨大的悖论。但是他们的困惑来自于他们的观点一一他们只认为是“00”=-1”.是的,Re(i)Re(i)=0,但那不是运算!我们要Re(i*i),完全不一样!我们在它自己的维度上平方I,然后把结果带回我们的维度。我们需要的是虚数I的平方,而不是我们心目中的0。
小心微积分中类似的错误:我们处理看起来像sro的微小数字,但我们不能假设它们是数学(就像对待I像0一样)。不,我们需要在另一个维度“做数学”并将结果转换回来。
极限和无穷小对于如何进行这种转换有不同的观点:
- 极限:在你察觉不到的精度水平上“算一算”(毫米),然后把它还原成你的刻度上的数字(英寸)
- 无穷小:在不同的维度中“做数学题”,并把它带回“标准”维度(就像取复数的实部一样:你取一个超实数的“标准”部分一一稍后再讲)
从来没有人告诉我:微积分让你用更简单的模型以更高的精度工作,并把结果带回
我们的世界。
真实的例子:sin(x)/x让我们尝试一个概念性的例子。假设我们想知道si(x)发生了什么/x为零。现在,如果我们代入x=0,我们得到一个无意义的结果:sin(0)=0,所以我们得到0/0,它可以是任何值。
让我们退一步:在我们的世界里,“x=0”意味着什么?好吧,如果我们允许存在更高水平的准确性,我们知道:
- 看起来为零的东西在不同的维度上可能是非零的(就像我可能看起来是零,但实际上不是)
我们会说,在这个更高的精度水平上,x可以非常非常接近于零,但不是“真零”。直觉上,你可以认为x是0.0000..00001,那里的“…”有足够多的零让你不再能发现这个数字。(在极限条件下,我们说x=0+d(delta,一个使我们保持在误差范围内的小变化),在无穷小条件下,我们说x=0+h,其中h是一个微小的超实数,称为无穷小)
好,我们有x在“对我们来说是零,但不是真的”。现在我们需要一个更简单的sin(x)模型。为什么?正弦是一条疯狂重复的曲线,很难知道发生了什么。但事实证明,在短距离内,直线是一个非常好的曲线模型:

就像我们可以将一个填充的形状分解成小矩形来简化它一样,我们可以将一条曲线分解成一系列线段。在0附近,si(x)看起来像线“x”。所以,我们把sin(x)换成线“x”。新的比例是多少?
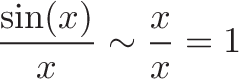
嗯,“x/x”是1。记住,我们不是真的被零除,因为在这个超级精确的世界里:x很小但不为零(0+d,或0+)。当我们“取极限”或“取标准部分”时,这意味着我们计算(x/x=1),然后找到世界上最接近的数字(1等于1)。
因此,当sin(x)/x接近零时,我们得到1,也就是说,我们使x尽可能小,因此对我们来说它变成0。如果x变成纯的,真正的零,那么比率将是未定义的(而且是在无穷小的水平!).但是我们永远不确定我们是否处于完美的零度一一大约0.0000...0001对我们来说就像零。所以,就我们所知,“sin(x)/x”看起来像“x/x=1”。直观地说,一旦我们读到弧度,这个结果就有意义了)。
可视化流程
今天的目标不是解决极限问题,而是理解解决它们的过程。为了解决这个例子:
- 认识到x=0从我们的精度是达不到的:一个“小但不为零”的x总是在更高的精度水平上可用
- 用直线代替sin(x)作为更简单的模型
- 用更简单的模型(x/x=1)进行“计算”
- 将结果(1)带回我们的准确度(保持1)以下是我
对这个过程的看法:

在后面的文章中,我们将学习建立和求解模型的细节。
警告:这个技巧并不总是奏效有些函数真的很不稳定”一一它们可能在无穷小的水平上有所不同。这意味着我们不能可靠地把他们带回我们的世界。看起来函数在微观层次上不稳定,表现得不“平稳”。极限的严格部分是计算出哪些函数表现得足够好,可以建立简单而精确的模型。幸运的是,世界上大多数自然函数(x,x2,sin,e^)表现良好,cm可以用微积分来建模。
极限还是无穷小?
从逻辑上讲,这两种方法都解决了“零和非零”的问题。我喜欢无穷小,因为它们允许“另一个维度”,这似乎比“总是在你伸手可及的范围之外”更清晰的分离。无穷小是微积分直觉的基础,出现在物理学和其他使用它的学科中。这不是分析课,但数学机器人可以放心,无穷小有一个严格的基础。我使用它们是因为它们为我而点击。
总结:
唷!有些想法很复杂,我觉得我是在说两面话:我们希望更简单,但仍然非常准确?
这个著名的关于“有时为零,其他时候非零”的两难问题是微积分的一个著名的批判。自从结果出来后,它基本上被忽略了,但是在19世纪,限制被引入以真正解决这个难题。我们今天学习了极限,但是不理解他们试图解决的问题的本质!
以下是关键概念:
- 零是相对的:有些东西对我们来说可能是零,而在其他地方可能不是零
- 无穷小(“另一个维度”)和极限(“超出我们的准确度”)解决了“零和非零”的困境
- 我们在更精确的维度上创建更简单的模型,进行数学运算,并将结果带到我们的世界
- 最终结果对我们来说是完全准确的
我的目标不是做数学,而是理解它。微积分的很大一部分是意识到超出我们精确度的简单模型在我们的维度上看起来“很好”。稍后,我们将学习构建和使用这些模型的规则。快乐数学。