悬线法可以用来解决给定矩阵极大子矩阵问题。

洛谷 P4147 玉蟾宫

这题本质上就是给定一个矩阵，有一些格不能选，求能选的最大的子矩阵大小，可以用悬线法来解决。

悬线，指的是从某一点向上出发，不穿过任何障碍格的垂直线段。比如下图中的几条悬线：

有一个结论：最大子矩阵一定可以通过某条悬线向左右拓展而成（可能有多条可能的悬线）。其实这个结论也很好证明，因为矩阵一定是被框在边界或障碍物之间，那么拓展成这个矩阵的悬线就是到其下界在框它上面的障碍物的那条线，否则一定有更优的矩阵。

知道了这个，我们就可以枚举每一条悬线，求出它能拓展的最大矩阵求个 \(\max\)。由于只有 \(nm\) 条悬线，所以理论上是可以做到 \(O(nm)\) 的时间复杂度的。

接下来看具体操作。

悬线悬线，肯定要维护线的长度。记 \(up_{i,j}\) 为从 \((i,j)\) 出发的悬线的长度，则：若 \((i,j)\) 不为障碍物，则其为 \(up_{i-1,j}+1\)；否则为 \(0\)。这个很好理解，就是不是障碍物的话应该比上面的格子长度多 \(1\)。

接下来还需要知道悬线能拓展到哪里。线不好维护，那就先考虑点，然后“连点成线”：\(l_{i,j}\) 表示 \((i,j)\) 这个点能向左拓展的最长长度（包括本身），\(r_{i,j}\) 表示其能向右拓展的最长长度，转移和上面类似，如果 \((i,j)\) 不为障碍物则 \(l_{i,j}=l_{i,j-1}+1,r=r_{i,j+1}+1\)，否则均为 \(0\)。

这一部分的代码：

for (int i = 1; i <= n; i++) {
	for (int j = 1; j <= m; j++) {
	    if (a[i][j] != 'R')
		    up[i][j] = up[i - 1][j] + 1, l[i][j] = l[i][j - 1] + 1;
	}
	for (int j = m; j >= 1; j--) //求 r 数组要倒序枚举
		if (a[i][j] != 'R') r[i][j] = r[i][j + 1] + 1; 
}

然后就需要回归正题：求悬线的拓展。即 \(L_{i,j},R_{i,j}\) 表示 \((i,j)\) 这条悬线能拓展到哪里，还是分情况讨论（以 \(L\) 为例）：

若 \(a_{i-1,j}\) 是障碍点，那么它就只能在本行拓展，答案就是 \(l_{i,j}\)；否则相当于 \((i-1,j)\) 的悬线和 \((i,j)\) 这个点一起拓展，显然就是 \(\min(L_{i-1,j},l_{i-1,j})\)。

统计最终的答案就很简单了。就是枚举每条悬线算面积：\(ans=\max\{up_{i,j}\times (L_{i,j}+R_{i,j}-1)\}\)。注意本题答案需要乘 \(3\)。

在代码实现中，\(l,L\)、\(r,R\) 可以合并成一个数组：

#include <bits/stdc++.h>
using namespace std;
const int N = 1005;
char a[N][N];
int up[N][N], l[N][N], r[N][N];
int main() {
	int n, m; cin >> n >> m;
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++)
			cin >> a[i][j];
	for (int i = 1; i <= n; i++) {
    	for (int j = 1; j <= m; j++) {
            if (a[i][j] != 'R')
        	    up[i][j] = up[i - 1][j] + 1, l[i][j] = l[i][j - 1] + 1;
        }
        for (int j = m; j >= 1; j--) 
        	if (a[i][j] != 'R') r[i][j] = r[i][j + 1] + 1; 
        }
	int ans = 0;
	for (int i = 0; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			if (!i) {
				l[i][j] = r[i][j] = m;//0 的情况要预处理为最大值
				continue;
			}
			if (a[i - 1][j] != 'R') {//是 R 的话不变
				l[i][j] = min(l[i][j], l[i - 1][j]);
				r[i][j] = min(r[i][j], r[i - 1][j]);
			}	
			if (a[i][j] != 'R') //不为障碍点的时候才能更新答案
				ans = max(ans, (r[i][j] + l[i][j] - 1) * up[i][j]);
		}
	}	
	cout << 3 * ans;//最后记得乘 3
	return 0; 
}

洛谷 P1169 棋盘制作

题目简述：求 01 矩阵中最大的 01 交错的正方形和矩形大小。

其实总的思路和这个上一题差不多，可以练练手。

数组啥的都一样，就是求 \(l,r,up\) 时的条件变成了 01 交错：

for (int i = 1; i <= n; i++) {
	for (int j = 1; j <= m; j++) {
		if (a[i][j] != a[i - 1][j]) up[i][j] = up[i - 1][j] + 1;
		else up[i][j] = 1;
		if (a[i][j] != a[i][j - 1]) l[i][j] = l[i][j - 1] + 1; 
		else l[i][j] = 1;
	}
	for (int j = m; j >= 1; j--) {
		if (a[i][j] != a[i][j + 1]) r[i][j] = r[i][j + 1] + 1;
		else r[i][j] = 1;
	}
} 

统计答案的地方稍有变动：

for (int i = 1; i <= n; i++) {
	for (int j = 1; j <= m; j++) {
		if (i != 1 && a[i][j] != a[i - 1][j]) {
			l[i][j] = min(l[i][j], l[i - 1][j]);
			r[i][j] = min(r[i][j], r[i - 1][j]);
		}
		//这里无论 a[i][j] 是什么都可以统计 
		ans1 = max(ans1, min(up[i][j], l[i][j] + r[i][j] - 1) * min(up[i][j], l[i][j] + r[i][j] - 1));
		//正方形就是悬线长度和拓展长度取一个 min 的平方 
		ans2 = max(ans2, up[i][j] * (l[i][j] + r[i][j] - 1));
	}
}

总的来说几乎一模一样。

洛谷 P1578 奶牛浴场

题目简述：求最大的不覆盖给定点（可以在边上）的子矩阵。

这题乍一看和上面几乎一样，但是一看数据范围：\(1\le L,W\le 5\times 10^4\)，这不是连数组都开不下？再一看障碍点的个数：\(1\le n\le 5\times 10^3\)，这暗示着可以用 \(O(n^2)\) 的复杂度来解决这个问题。

如何解决呢？这里就要用到极大化思想了。首先要明确的是，最大子矩阵一定是被障碍点或边界“框”着的，这点在上面也有提到过。而其实真正起到控制作用的只有四个点或边框（相同边框的任取一个），这就引导我们通过枚举这些点或边框来确定矩阵，为了避免一些边界问题，我们把边框化成点：

int n, m, s; cin >> m >> n >> s;
for (int i = 1; i <= s; i++)
	cin >> a[i].y >> a[i].x;
a[++s] = {0, 0};//分别对应了大矩阵的四个角 
a[++s] = {0, m};
a[++s] = {n, 0};
a[++s] = {n, m};

回到上面的话题，直接枚举四个点显然不可行，但是可以发现，当高/宽的两点确定之后（这里和下面的“高”/“宽”指的都是边而不是长度），另外两点也随之确定：它们之间的最“内”的障碍点（如果没有的话就是边界）。以确定高的两点为例：

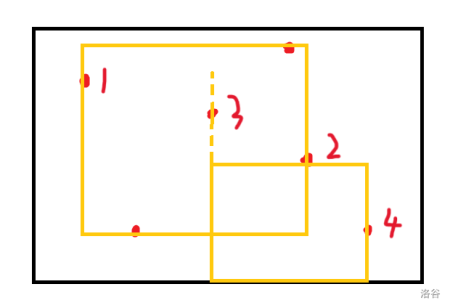
上面的两个矩阵，就是分别以 \(1,2\) 和 \(3,4\) 为两条高的边界。注意到，这些点不一定在矩阵（指小矩阵）的边框上。

当然，其实情况还有一种，就是大矩阵的边界作为小矩阵的高，这点也得注意。

思路基本说明白了，但是实践到代码里还是会有不同，步骤如下（这里以确定高为例）（统一一下，下文的 \(n,m\) 指的是题目中的 \(W,L\)（宽和长），\(s\) 指的是障碍点个数，\((x,y)\) 这个点默认指的是第 \(x\) 行第 \(y\) 列而不是第 \(x\) 列第 \(y\) 行）：

1. 把所有障碍点（包括边界）按 \(y\) 排序；

2. 枚举每个障碍点当作左边的高，向右延伸到每一个点，并在延伸过程中实时统计当前矩阵的“上界”和“下界”;

3. 从右往左再扫一遍；

4. 把所有障碍点按 \(x\) 排序，统计以边界为高的情况。

#include <bits/stdc++.h>
using namespace std;
const int N = 5e3 + 5; 
struct node {
	int x, y;
}a[N];
bool cmp1(node x, node y) {
	return x.x < y.x;
}
bool cmp2(node x, node y) {
	return x.y < y.y;
}
int main() {
	int n, m, s; cin >> m >> n >> s;//行列不要搞反了 
	for (int i = 1; i <= s; i++)
		cin >> a[i].y >> a[i].x;//同上 
	a[++s] = {0, 0}, a[++s] = {0, m}, a[++s] = {n, 0}, a[++s] = {n, m};
	sort(a + 1, a + 1 + s, cmp1);//先按行排序，统计特殊情况 
	int ans = 0;
	for (int i = 1; i <= s; i++)
		ans = max(ans, (a[i].x - a[i - 1].x) * m);
	sort(a + 1, a + 1 + s, cmp2);//再按列排序，统计一般情况 
	for (int i = 1; i <= s; i++) {
		int up = 0, down = n;//up 是上边界，down 是下边界 
		for (int j = i + 1; j <= s; j++) {//枚举向右的点 
			ans = max(ans, (down - up) * (a[j].y - a[i].y));//先统计答案再更新边界 
			if (a[j].x < a[i].x) up = max(up, a[j].x);//在上部分就更新上边界 
			else down = min(down, a[j].x);//否则更新下边界 
		}
	}
	for (int i = s; i >= 1; i--) {//这个和上面差不多，就是方向反过来 
		int up = 0, down = n;
		for (int j = i - 1; j >= 1; j--) {
			ans = max(ans, (down - up) * (a[i].y - a[j].y));
			if (a[j].x < a[i].x) up = max(up, a[j].x);
			else down = min(down, a[j].x);
		}
	}
	cout << ans;
	return 0;
}

题目描述：输入一个 01 矩形，对于每个 0 位，求出假设将其变成 1 后的得到最大全 0 子矩形大小，输出所有 0 位置的 \((x+y)ans_{x,y}\) 的异或和，\(1\le n, m\le 3000\)。

数据范围表明了我们可以选用 \(O(nm)\) 的算法。对于每个 0 点，不难发现，其实把它变成 1 后最终的答案就是它“四周”的矩阵中的最大全 0 子矩阵大小。说得可能有点不清楚，看图：

橙色点的答案就是粉、黄、绿、蓝四个矩阵中最大全零子矩阵的最大值。看上去这就要 \(O(nm)\) 了，观察到，需要的其实都是 \(1\sim i\) 行/列，\(i\sim n/m\) 行/列（称之为前/后缀），加下发现一开始我们对于一个大矩阵的统计是“有序的”，也就是一行一行来的，也就是其实就是依次求出每一个前/后缀，所以其实预处理只需要 \(O(nm)\)。

枚举答案很简单，而为了减少预处理的码量，可以只写一个函数求 \(1\sim i\) 行，剩下的每次将矩阵旋转 \(90^\circ\) 就可以用同一个函数求出。具体细节见代码：

#include <bits/stdc++.h>
using namespace std;
const int N = 3005;
int up[N][N], l[N][N], r[N][N];
inline void solve(int n, int m, int a[][N], int ans[]) {
	memset(up, 0, sizeof(up));//记得清空 
	memset(l, 0, sizeof(l));
	memset(r, 0, sizeof(r));
	for (int i = 1; i <= n; i++) {//这里和之前完全一样 
        for (int j = 1; j <= m; j++)
            if (!a[i][j]) up[i][j] = up[i - 1][j] + 1, l[i][j] = l[i][j - 1] + 1;
        for (int j = m; j >= 1; j--) 
            if (!a[i][j]) r[i][j] = r[i][j + 1] + 1; 
	}
    for (int i = 1; i <= n; i++) {
    	ans[i] = ans[i - 1];//前缀所以可以是上一行的贡献 
        for (int j = 1; j <= m; j++) {
            if (!a[i - 1][j] && i > 1) {
                l[i][j] = min(l[i][j], l[i - 1][j]);
                r[i][j] = min(r[i][j], r[i - 1][j]);
            }  
            if (!a[i][j]) ans[i] = max(ans[i], (int)(r[i][j] + l[i][j] - 1) * up[i][j]);
        }
    }   
}
inline void turn(int n, int m, int a[][N], int b[][N]) {//作用是将 a 矩阵旋转 90 度后存在 b 数组中
	//传入的 n,m 是 a 矩阵的行列 
	for (int i = 1; i <= m; i++)
		for (int j = 1; j <= n; j++)
			b[i][j] = a[j][i];
	for (int i = 1; i <= m; i++)
		for (int j = 1; j <= n / 2; j++)
			swap(b[i][j], b[i][n - j + 1]);
}
int a[N][N], b[N][N], ans1[N], ans2[N], ans3[N], ans4[N];//ans 数组分别为 上左下右的前缀和 
signed main() {
	int n, m; cin >> n >> m;
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++) {
			char x; cin >> x;
			a[i][j] = x - '0';
		}
	//下面是轮流使用 a,b 数组 
	solve(n, m, a, ans1); 
	turn(n, m, a, b);
	solve(m, n, b, ans2);//注意此时 n,m 要反过来 
	turn(m, n, b, a);
	solve(n, m, a, ans3);
	turn(n, m, a, b);	
	solve(m, n, b, ans4);
	turn(m, n, b, a);
	int ans = 0;
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++)//有的不是直接 i/j 带入，要小心 
			if (a[i][j] == 0) ans ^= (i + j) * max({ans1[i - 1], ans4[m - j], ans3[n - i], ans2[j - 1]});
	cout << ans;	
	return 0;
}

\(\mathcal{The\text{ }End.}\)

热门相关：嫁偶天成   异能特工：军火皇后   紫府仙缘   我成了暴戾帝君的小娇包   楚氏赘婿