FSCTF 2023(公开赛道)CRYPTO WP
RSA 1
1、题目信息
提交格式:FSCTF{你所解出的内容}p=1458769258361
q=4556983871563
e=17
求d2、解题方法
exp
from gmpy2 import *
p=1458769258361
q=4556983871563
e=17
d = int(invert(e, (p-1)*(q-1)))
print(d)
#FSCTF{5865518808244394324786753}做不出来就别阴阳怪气啦
1、题目信息
啊这?不是吧?就这啊?做不了啊?做不出来就别阴阳怪气啦就 这 ¿ 就 这 ¿ 不 会 吧 ? 就 这 ¿ 就 这 ¿ 就 这 ¿ 不 会 吧 ? 不 会 吧 ? 就 这 ¿ 就 这 ¿ 就 这 ¿ 不 会 吧 ? 就 这 ¿ 不 会 吧 ? 就 这 ¿ 就 这 ¿ 不 会 吧 ? 不 会 吧 ? 就 这 ¿ 就 这 ¿ 不 会 吧 ? 就 这 ¿ 就 这 ¿ 就 这 ¿ 就 这 ¿ 不 会 吧 ? 不 会 吧 ? 就 这 ¿ 就 这 ¿ 不 会 吧 ? 就 这 ¿ 不 会 吧 ? 就 这 ¿ 不 会 吧 ? 就 这 ¿ 就 这 ¿ 就 这 ¿ 就 这 ¿ 不 会 吧 ? 就 这 ¿ 就 这 ¿ 就 这 ¿ 不 会 吧 ? 不 会 吧 ? 就 这 ¿ 就 这 ¿ 就 这 ¿ 不 会 吧 ? 不 会 吧 ? 不 会 吧 ? 不 会 吧 ? 就 这 ¿ 不 会 吧 ? 不 会 吧 ? 就 这 ¿ 就 这 ¿ 不 会 吧 ? 就 这 ¿ 就 这 ¿ 不 会 吧 ? 就 这 ¿ 不 会 吧 ? 就 这 ¿ 就 这 ¿ 就 这 ¿ 不 会 吧 ? 不 会 吧 ? 就 这 ¿ 不 会 吧 ? 就 这 ¿ 就 这 ¿ 不 会 吧 ? 就 这 ¿ 就 这 ¿ 不 会 吧 ? 不 会 吧 ? 不 会 吧 ? 就 这 ¿ 不 会 吧 ? 就 这 ¿ 不 会 吧 ? 就 这 ¿ 就 这 ¿ 不 会 吧 ? 不 会 吧 ? 不 会 吧 ? 不 会 吧 ? 就 这 ¿ 不 会 吧 ? 就 这 ¿ 就 这 ¿ 就 这 ¿ 不 会 吧 ? 不 会 吧 ? 就 这 ¿ 不 会 吧 ? 就 这 ¿ 就 这 ¿ 就 这 ¿ 就 这 ¿ 就 这 ¿ 不 会 吧 ? 不 会 吧 ? 就 这 ¿ 就 这 ¿ 不 会 吧 ? 就 这 ¿ 不 会 吧 ? 就 这 ¿ 就 这 ¿ 不 会 吧 ? 就 这 ¿ 就 这 ¿ 就 这 ¿ 就 这 ¿ 就 这 ¿ 就 这 ¿ 就 这 ¿ 就 这 ¿ 不 会 吧 ? 就 这 ¿ 就 这 ¿ 不 会 吧 ? 就 这 ¿ 不 会 吧 ? 就 这 ¿ 就 这 ¿ 就 这 ¿ 不 会 吧 ? 不 会 吧 ? 不 会 吧 ? 就 这 ¿ 不 会 吧 ? 就 这 ¿ 不 会 吧 ? 就 这 ¿ 就 这 ¿ 不 会 吧 ? 不 会 吧 ? 不 会 吧 ? 就 这 ¿ 就 这 ¿ 不 会 吧 ? 不 会 吧 ? 就 这 ¿ 就 这 ¿ 不 会 吧 ? 不 会 吧 ? 不 会 吧 ? 就 这 ¿ 不 会 吧 ? 就 这 ¿ 就 这 ¿ 就 这 ¿ 就 这 ¿ 不 会 吧 ? 就 这 ¿ 不 会 吧 ? 就 这 ¿ 就 这 ¿ 不 会 吧 ? 不 会 吧 ? 就 这 ¿ 就 这 ¿ 不 会 吧 ? 不 会 吧 ? 就 这 ¿ 不 会 吧 ? 不 会 吧 ? 不 会 吧 ? 不 会 吧 ? 就 这 ¿ 就 这 ¿ 不 会 吧 ? 就 这 ¿ 不 会 吧 ? 就 这 ¿ 就 这 ¿ 不 会 吧 ? 不 会 吧 ? 就 这 ¿ 就 这 ¿ 不 会 吧 ? 不 会 吧 ? 就 这 ¿ 不 会 吧 ? 不 会 吧 ? 不 会 吧 ? 不 会 吧 ? 就 这 ¿ 就 这 ¿ 不 会 吧 ? 不 会 吧 ? 不 会 吧 ? 不 会 吧 ? 不 会 吧 ? 就 这 ¿ 不 会 吧 ? 2、解题方法
阴阳怪气密码解码
FSCTF{Jiuzhe@JustSoSo}RSA 2
1、题目信息
提交格式:FSCTF{你所解出的内容}c=90362297576572826064831133206230135349790392078780406000643496612200873754835039374184323808342127071833274981191134125413478105835272238356352724573228797863805124195170088819735610736936895478614898105848968069280022022112207095140266709372221090586917729998024205978412679448008696923580889787529663283314
p=8637633767257008567099653486541091171320491509433615447539162437911244175885667806398411790524083553445158113502227745206205327690939504032994699902053229
q=11874843837980297032092405848653656852760910154543380907650040190704283358909208578251063047732443992230647903887510065547947313543299303261986053486569407
e=655372、解题方法
import gmpy2
from Crypto.Util.number import long_to_bytes
c=90362297576572826064831133206230135349790392078780406000643496612200873754835039374184323808342127071833274981191134125413478105835272238356352724573228797863805124195170088819735610736936895478614898105848968069280022022112207095140266709372221090586917729998024205978412679448008696923580889787529663283314
p=8637633767257008567099653486541091171320491509433615447539162437911244175885667806398411790524083553445158113502227745206205327690939504032994699902053229
q=11874843837980297032092405848653656852760910154543380907650040190704283358909208578251063047732443992230647903887510065547947313543299303261986053486569407
e=65537
phi = (p-1) * (q-1)
n = p * q
d = gmpy2.invert(e, phi)
m = pow(c, d, n)
print(m)
#FSCTF{20230824}RSA 3
1、题目信息
提交格式:FSCTF{你所解出的内容}from Crypto.Util.number import bytes_to_long
m=bytes_to_long(flag)
n= 12308543373374311860115195114269947739026255098864232126071500623399852788903738569949462616714391748269539072128882946132686996592089735285396762634029371785959865779256901123369306119124563405765293657606975290441243965513640680841871955014230301486214824204887945375140818283280272607903500556306646445508386218951500563603482945071727344737690804338144982687000734071274618240408238519378280819162796749148066754028700125846348589164721591354555019608871411236973606149388257533629388508942271702742078883636357856776193846813894734271905070538713351614750057245897158615891962167410053552739441195871000310777649
e= 65537
dp= 28196759050232165736649945458463681080421101473761579424309687746007021074159564720195299959516638110870101025657932732247788828322476803386736345945717104030991724584628153257976163663460034720811420324255626233108130037584679035250792445830510130682783638394418531763109219293027733347554816808577799709553
c= 18557982570442382803270424558327858897631412348831804041585550714430886301130340330504092595136323437426655440434378309597508734319289809102363980266709451843289506925681138198216996964184381573362637998084046987954332439685362567803969109146929494845569504917225276617062550098634819055903717250895873770650003541093960623604400214476074016870822477754533691174248489273868574250510979319837039662536529211139203870080480243087936866439444045419411829979638735799886809655585818852731857215766680014628171502459556282932585120243235155810632352486272231791175495405416421858154899780893670611029201143958713290232082、解题方法
dp泄露
exp
import gmpy2 as gp
e = 65537
n = gp.mpz(12308543373374311860115195114269947739026255098864232126071500623399852788903738569949462616714391748269539072128882946132686996592089735285396762634029371785959865779256901123369306119124563405765293657606975290441243965513640680841871955014230301486214824204887945375140818283280272607903500556306646445508386218951500563603482945071727344737690804338144982687000734071274618240408238519378280819162796749148066754028700125846348589164721591354555019608871411236973606149388257533629388508942271702742078883636357856776193846813894734271905070538713351614750057245897158615891962167410053552739441195871000310777649)
dp = gp.mpz(28196759050232165736649945458463681080421101473761579424309687746007021074159564720195299959516638110870101025657932732247788828322476803386736345945717104030991724584628153257976163663460034720811420324255626233108130037584679035250792445830510130682783638394418531763109219293027733347554816808577799709553)
c = gp.mpz(1855798257044238280327042455832785889763141234883180404158555071443088630113034033050409259513632343742665544043437830959750873431928980910236398026670945184328950692568113819821699696418438157336263799808404698795433243968536256780396910914692949484556950491722527661706255009863481905590371725089587377065000354109396062360440021447607401687082247775453369117424848927386857425051097931983703966253652921113920387008048024308793686643944404541941182997963873579988680965558581885273185721576668001462817150245955628293258512024323515581063235248627223179117549540541642185815489978089367061102920114395871329023208
)
for x in range(1, e):
if(e*dp%x==1):
p=(e*dp-1)//x+1
if(n%p!=0):
continue
q=n//p
phin=(p-1)*(q-1)
d=gp.invert(e, phin)
m=gp.powmod(c, d, n)
if(len(hex(m)[2:])%2==1):
continue
print('--------------')
print(m)
print(hex(m)[2:])
print(bytes.fromhex(hex(m)[2:]))
#FSCTF{Cheese_snow_1eop@rd}Big_e
1、题目信息
这么大的e吗?n = 12238605063252292170613110607692779326628090745751955692266649177882959231822580682548279800443278979485092243645806337103841086023159482786712759291169541633901936290854044069486201989034158882661270017305064348254800318759062921744741432214818915527537124001063995865927527037625277330117588414586505635959411443039463168463608235165929831344586283875119363703480280602514451713723663297066810128769907278246434745483846869482536367912810637275405943566734099622063142293421936734750356828712268385319217225803602442033960930413469179550331907541244416573641309943913383658451409219852933526106735587605884499707827
e= 11850552481503020257392808424743510851763548184936536180317707155841959788151862976445957810691568475609821000653594584717037528429828330763571556164988619635320288125983463358648887090031957900011546300841211712664477474767941406651977784177969001025954167441377912326806132232375497798238928464025466905201977180541053129691501120197010080001677260814313906843670652972019631997467352264392296894192998971542816081534808106792758008676039929763345402657578681818891775091140555977382868531202964486261123748663752490909455324860302967636149379567988941803701512680099398021640317868259975961261408500449965277690517
c=4218884541887711839568615416673923480889604461874475071333225389075770098726337046768413570546617180777109293884545400260353306419150066928226964662256930702466709992997796154415790565112167663547017839870351167884417142819504498662037048412313768450136617389372395690363188005647619061128497371121168347810294424378348301835826084732747005110258557662466626720961279087145559906371505117097599774430970980355531235913439823966628008554872896820907555353892843539526041019103819804854883231421963308265517622470779089941078841902464033685762524196275032288319744157255628189204988632871276637699312750636348750883054
请解出明文!!!2、解题方法
exp1:维纳攻击1
# Sage
def rational_to_contfrac(x, y):
# Converts a rational x/y fraction into a list of partial quotients [a0, ..., an]
a = x // y
pquotients = [a]
while a * y != x:
x, y = y, x - a * y
a = x // y
pquotients.append(a)
return pquotients
def convergents_from_contfrac(frac):
# computes the list of convergents using the list of partial quotients
convs = [];
for i in range(len(frac)): convs.append(contfrac_to_rational(frac[0: i]))
return convs
def contfrac_to_rational(frac):
# Converts a finite continued fraction [a0, ..., an] to an x/y rational.
if len(frac) == 0: return (0, 1)
num = frac[-1]
denom = 1
for _ in range(-2, -len(frac) - 1, -1): num, denom = frac[_] * num + denom, num
return (num, denom)
n = 12238605063252292170613110607692779326628090745751955692266649177882959231822580682548279800443278979485092243645806337103841086023159482786712759291169541633901936290854044069486201989034158882661270017305064348254800318759062921744741432214818915527537124001063995865927527037625277330117588414586505635959411443039463168463608235165929831344586283875119363703480280602514451713723663297066810128769907278246434745483846869482536367912810637275405943566734099622063142293421936734750356828712268385319217225803602442033960930413469179550331907541244416573641309943913383658451409219852933526106735587605884499707827
e= 11850552481503020257392808424743510851763548184936536180317707155841959788151862976445957810691568475609821000653594584717037528429828330763571556164988619635320288125983463358648887090031957900011546300841211712664477474767941406651977784177969001025954167441377912326806132232375497798238928464025466905201977180541053129691501120197010080001677260814313906843670652972019631997467352264392296894192998971542816081534808106792758008676039929763345402657578681818891775091140555977382868531202964486261123748663752490909455324860302967636149379567988941803701512680099398021640317868259975961261408500449965277690517
c= 4218884541887711839568615416673923480889604461874475071333225389075770098726337046768413570546617180777109293884545400260353306419150066928226964662256930702466709992997796154415790565112167663547017839870351167884417142819504498662037048412313768450136617389372395690363188005647619061128497371121168347810294424378348301835826084732747005110258557662466626720961279087145559906371505117097599774430970980355531235913439823966628008554872896820907555353892843539526041019103819804854883231421963308265517622470779089941078841902464033685762524196275032288319744157255628189204988632871276637699312750636348750883054
def egcd(a, b):
if a == 0: return (b, 0, 1)
g, x, y = egcd(b % a, a)
return (g, y - (b // a) * x, x)
def mod_inv(a, m):
g, x, _ = egcd(a, m)
return (x + m) % m
def isqrt(n):
x = n
y = (x + 1) // 2
while y < x:
x = y
y = (x + n // x) // 2
return x
def crack_rsa(e, n):
frac = rational_to_contfrac(e, n)
convergents = convergents_from_contfrac(frac)
for (k, d) in convergents:
if k != 0 and (e * d - 1) % k == 0:
phi = (e * d - 1) // k
s = n - phi + 1
# check if x*x - s*x + n = 0 has integer roots
D = s * s - 4 * n
if D >= 0:
sq = isqrt(D)
if sq * sq == D and (s + sq) % 2 == 0: return d
d = crack_rsa(e, n)
m = hex(pow(c, d, n))[2:]
print(bytes.fromhex(m))
#FSCTF{Y0u_ar3_s0_C001}exp2:维纳攻击2
import gmpy2
def transform(x, y): # 使用辗转相处将分数 x/y 转为连分数的形式
res = []
while y:
res.append(x // y)
x, y = y, x % y
return res
def continued_fraction(sub_res):
numerator, denominator = 1, 0
for i in sub_res[::-1]: # 从sublist的后面往前循环
denominator, numerator = numerator, i * numerator + denominator
return denominator, numerator # 得到渐进分数的分母和分子,并返回
# 求解每个渐进分数
def sub_fraction(x, y):
res = transform(x, y)
res = list(map(continued_fraction, (res[0:i] for i in range(1, len(res))))) # 将连分数的结果逐一截取以求渐进分数
return res
def get_pq(a, b, c): # 由p+q和pq的值通过维达定理来求解p和q
par = gmpy2.isqrt(b * b - 4 * a * c) # 由上述可得,开根号一定是整数,因为有解
x1, x2 = (-b + par) // (2 * a), (-b - par) // (2 * a)
return x1, x2
def wienerAttack(e, n):
for (d, k) in sub_fraction(e, n): # 用一个for循环来注意试探e/n的连续函数的渐进分数,直到找到一个满足条件的渐进分数
if k == 0: # 可能会出现连分数的第一个为0的情况,排除
continue
if (e * d - 1) % k != 0: # ed=1 (mod φ(n)) 因此如果找到了d的话,(ed-1)会整除φ(n),也就是存在k使得(e*d-1)//k=φ(n)
continue
phi = (e * d - 1) // k # 这个结果就是 φ(n)
px, qy = get_pq(1, n - phi + 1, n)
if px * qy == n:
p, q = abs(int(px)), abs(int(qy)) # 可能会得到两个负数,负负得正未尝不会出现
d = gmpy2.invert(e, (p - 1) * (q - 1)) # 求ed=1 (mod φ(n))的结果,也就是e关于 φ(n)的乘法逆元d
return d
print("该方法不适用")
n = 12238605063252292170613110607692779326628090745751955692266649177882959231822580682548279800443278979485092243645806337103841086023159482786712759291169541633901936290854044069486201989034158882661270017305064348254800318759062921744741432214818915527537124001063995865927527037625277330117588414586505635959411443039463168463608235165929831344586283875119363703480280602514451713723663297066810128769907278246434745483846869482536367912810637275405943566734099622063142293421936734750356828712268385319217225803602442033960930413469179550331907541244416573641309943913383658451409219852933526106735587605884499707827
e= 11850552481503020257392808424743510851763548184936536180317707155841959788151862976445957810691568475609821000653594584717037528429828330763571556164988619635320288125983463358648887090031957900011546300841211712664477474767941406651977784177969001025954167441377912326806132232375497798238928464025466905201977180541053129691501120197010080001677260814313906843670652972019631997467352264392296894192998971542816081534808106792758008676039929763345402657578681818891775091140555977382868531202964486261123748663752490909455324860302967636149379567988941803701512680099398021640317868259975961261408500449965277690517
c=4218884541887711839568615416673923480889604461874475071333225389075770098726337046768413570546617180777109293884545400260353306419150066928226964662256930702466709992997796154415790565112167663547017839870351167884417142819504498662037048412313768450136617389372395690363188005647619061128497371121168347810294424378348301835826084732747005110258557662466626720961279087145559906371505117097599774430970980355531235913439823966628008554872896820907555353892843539526041019103819804854883231421963308265517622470779089941078841902464033685762524196275032288319744157255628189204988632871276637699312750636348750883054
d = wienerAttack(e, n)
print("d=", d)
m = hex(pow(c, d, n))[2:]
print(bytes.fromhex(m))
#FSCTF{Y0u_ar3_s0_C001}Do you know gcd?
1、题目信息
from Crypto.Util.number import *
from secret import flag
m1=bytes_to_long(flag[:16])
m2=bytes_to_long(flag[16:])
p=getPrime(1024)
q1=getPrime(1024)
q2=getPrime(1024)
n1=p*q1
n2=p*q2
e=65537
c1=pow(m1,e,n1)
c2=pow(m2,e,n2)
print("n1=",n1)
print("n2=",n2)
print("c1=",c1)
print("c2=",c2)
'''
n1= 18680935400842120133090782991548100098299141114788036098274292600814484762178879421175852824971602717084073867867453382415307589970440719890918576225495401632854107018246844209327118177917122236073227158593514362850629722223228335334773008682775987859295083444638923726449899310854161394586430943134469559429878238769266114132469166535509030877235272476877484918308883799496627699789051809542538091061550107526246728583019140703765888157806778516567048103700384849598143249322109207879381251223776896702362630437178664824125387477797876186939235800859102380783259361745143574493440078787931593394188675093506492640857
n2= 16308523133405725830120564525574438512803584148781960516042054284309437381876822602134185065101371986717984978566359252072738078020261823966208153922611063201149105749778596739692554295573408850719208215646167050188830459343054219856901871953140988948482577813730729085764541988120049026971705499798003225755018687242522370406495429425494022876627543617474873929054728724093702291448754458748923218635900061398716191201846139296921753782690468189409101899415028480878296408735247604084627019116374444335509072590669239349212479592499426230525792270750612371117196200786891891430446212938482959351978202358044864822577
c1= 534518909595318304521410713148076850830155521838755402438490325620155197496935820831936109252194297244161393310730073882257949954815312409974998733265641354273665213856408848764503848122264972023143474923678585167025591255034150826271791019266426616987355463111138963331008761826310757292765842789380409826387579098421126952331558360737102888876551724241978020305977032047901621477384392409864427091911872691182528938458750707982564581322551517287491916691010743390992018974168703956622998928457142606354825714033609199676987795174032254878017883605565760275857658822315970522114838062469258676628619381342357632179
c2= 10248394002302905069278122013496854496130190499518622376819239887579692634750808499513497018453473232140518824608976734237637842228035017757831938865937098325684711995382081489403971465596662585196007547659143066184546400992333479193424580690897692586491475768279754939199148642035267049092880715299621206567123356521609120801306358100326600900326310677054810032471472266402660807205675696110133573150125117412696328434523507708110949743705536889950671778501402435457354251761692098671783596194430798692942013503015764266392551048702428063161786512924608239609802040937400619384828550050291094616346317726139970219621
'''2、题目信息
共e攻击
import gmpy2
import binascii
e = 65537
n1= 18680935400842120133090782991548100098299141114788036098274292600814484762178879421175852824971602717084073867867453382415307589970440719890918576225495401632854107018246844209327118177917122236073227158593514362850629722223228335334773008682775987859295083444638923726449899310854161394586430943134469559429878238769266114132469166535509030877235272476877484918308883799496627699789051809542538091061550107526246728583019140703765888157806778516567048103700384849598143249322109207879381251223776896702362630437178664824125387477797876186939235800859102380783259361745143574493440078787931593394188675093506492640857
n2= 16308523133405725830120564525574438512803584148781960516042054284309437381876822602134185065101371986717984978566359252072738078020261823966208153922611063201149105749778596739692554295573408850719208215646167050188830459343054219856901871953140988948482577813730729085764541988120049026971705499798003225755018687242522370406495429425494022876627543617474873929054728724093702291448754458748923218635900061398716191201846139296921753782690468189409101899415028480878296408735247604084627019116374444335509072590669239349212479592499426230525792270750612371117196200786891891430446212938482959351978202358044864822577
c1= 534518909595318304521410713148076850830155521838755402438490325620155197496935820831936109252194297244161393310730073882257949954815312409974998733265641354273665213856408848764503848122264972023143474923678585167025591255034150826271791019266426616987355463111138963331008761826310757292765842789380409826387579098421126952331558360737102888876551724241978020305977032047901621477384392409864427091911872691182528938458750707982564581322551517287491916691010743390992018974168703956622998928457142606354825714033609199676987795174032254878017883605565760275857658822315970522114838062469258676628619381342357632179
c2= 10248394002302905069278122013496854496130190499518622376819239887579692634750808499513497018453473232140518824608976734237637842228035017757831938865937098325684711995382081489403971465596662585196007547659143066184546400992333479193424580690897692586491475768279754939199148642035267049092880715299621206567123356521609120801306358100326600900326310677054810032471472266402660807205675696110133573150125117412696328434523507708110949743705536889950671778501402435457354251761692098671783596194430798692942013503015764266392551048702428063161786512924608239609802040937400619384828550050291094616346317726139970219621
p = gmpy2.gcd(n1, n2)
q = n2 // p # 这里用n2求第二部分
phi = (p - 1) * (q - 1)
d = gmpy2.invert(e, phi)
m = gmpy2.powmod(c2, d, n2)
print(binascii.unhexlify(hex(m)[2:]))
q = n1 // p # 这里用n1求第一部分
phi = (p - 1) * (q - 1)
d = gmpy2.invert(e, phi)
m = gmpy2.powmod(c1, d, n1)
print(binascii.unhexlify(hex(m)[2:]))
#FSCTF{0hN0_Y0u_f1nd_th3_gcd!}埃塞克的秘密
1、题目信息
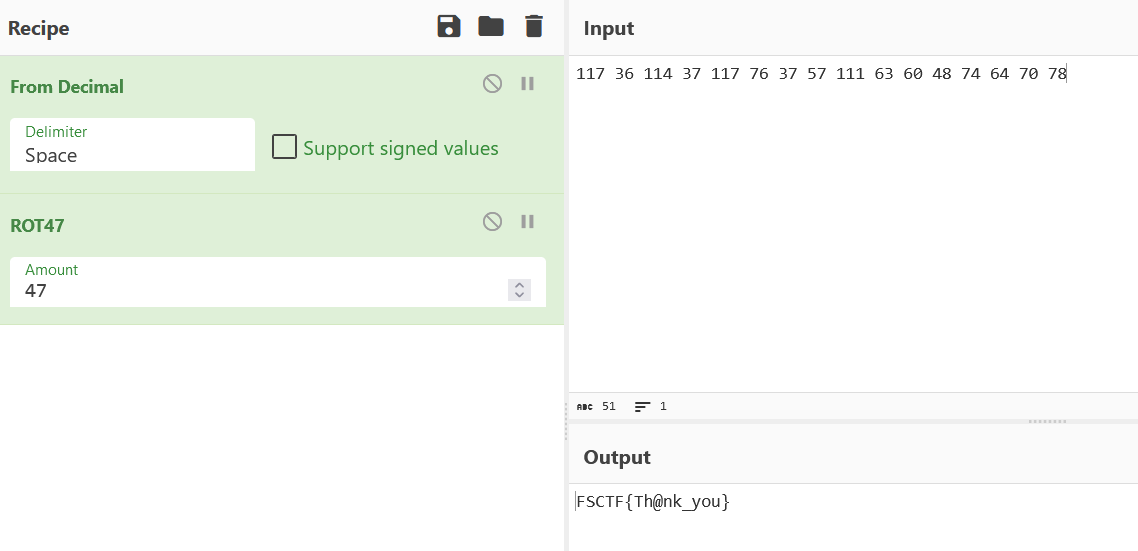
埃塞克先生将自己的秘密藏在盒子里并交给了ROT保管埃塞克先生将自己的秘密藏在盒子里并交给了ROT保管,埃塞克先生在盒子上留下了这样一串数字:
117 36 114 37 117 76 37 57 111 63 60 48 74 64 70 782、解题方法
cyber一把梭
RSA签到
1、题目信息
from Crypto.Util.number import *
from secret import flag
m = bytes_to_long(flag)
assert m.bit_length()<150
p = getPrime(512)
q = getPrime(512)
n = p*q
e = 3
c = pow(m, e, n)
kbits = 103
m = (m >> kbits) << kbits
Mod = getPrime(2048)
hint1 = (2019-2023*m) % Mod
hint2 = pow(2, 2023, Mod)
print('n =',n)
print('c =',c)
print('hint1 =',hint1)
print('hint2 =',hint2)
'''
n = 113369575322962228640839640796005129142256499725384495463316595604047079557930666699058024217561098997292782305151595366764483672240871690818579470888054811186902762990032505953330034837625667158114251720321766235335996441613828302393569643827293040591156144187232255906107532680524431761932215860898533224303
c = 42336544435252811021843650684098817755849747192874682997240960601474927692351510022965782272751339319782351146077580929125
hint1 = 23620186624579054670890922956929031966199853422018331906359817627553015939570302421768667351617160816651880338639432052134891008193969801696035505565684982786461527274477933881508678074157199742425764746919878452990468268098540220237611917321213668069666526658025737487539455262610713002399515462380573732082344497124344090365729168706760425585735014513373401622860196569544933971210142724734536588173957576667830667503151362930889494877201597267000737408071228466811160470759093928003064486766171850080985758351203536462206720715743059101285822169971058423075796415932349942113371706910521251120400151508125606778268
hint2 = 963121833542317369601573845406471251262548645428284526828835768327851746644612875378048462019053502788803516653832734212104068969204751285764221918179043624419894139984279754512017898273159626328827668380262481220865017731267802600915375183179264380651165421367773563947903391466768557089792263481734108493385146063258300495764165365295546337808852673629710735621386935094923561594142327134318905856137785813985574356271679918694447015294481691849341917432346559501502683303082591585074576786963085039546446281095048723669230856548339087909922753762884060607659880382812905450025751549153093939827557015748608
'''2、解题方法
看上去很复杂,但想一想flag也没多长,而e=3直接小明文开方即可。。。
exp
from Crypto.Util.number import long_to_bytes
from gmpy2 import iroot
c1 = 42336544435252811021843650684098817755849747192874682997240960601474927692351510022965782272751339319782351146077580929125
m = iroot(c1,3)[0]
print(long_to_bytes(m).decode())
#flag{sign_1n_RSA}ezRSA
1、题目信息
from Crypto.Util.number import *
from secret import flag
def keygen(nbit = 64):
while True:
k = getRandomNBitInteger(nbit)
p = k**6 + 7*k**4 - 40*k**3 + 12*k**2 - 114*k + 31377
q = k**5 - 8*k**4 + 19*k**3 - 313*k**2 - 14*k + 14011
if isPrime(p) and isPrime(q):
return p, q
def encrypt(msg, n, e = 31337):
m = bytes_to_long(msg)
return pow(m, e, n)
p, q = keygen()
n = p * q
enc = encrypt(flag, n)
print(f'n = {n}')
print(f'enc = {enc}')
'''
n = 1901485114700245088118015176838411045645808657633721129158322425051110390237801115516544893309422501851747092251796770953642000579931231478667887589988786560834446696408732292786254192492281586457284980263740183
enc = 1199361436656854951826843585559905358018072076349745598865984504434921942249797269971584270541920348511243191511578321283455075109027873358983934024677982086699270397304699932717071144314481599892879445599516848
'''2、解题方法
属于polyRSA——解单变量多项式方程
exp:
先用sage跑,求k
#sage跑
n = 1901485114700245088118015176838411045645808657633721129158322425051110390237801115516544893309422501851747092251796770953642000579931231478667887589988786560834446696408732292786254192492281586457284980263740183
enc = 1199361436656854951826843585559905358018072076349745598865984504434921942249797269971584270541920348511243191511578321283455075109027873358983934024677982086699270397304699932717071144314481599892879445599516848
k = var('k')
p = k**6 + 7*k**4 - 40*k**3 + 12*k**2 - 114*k + 31377
q = k**5 - 8*k**4 + 19*k**3 - 313*k**2 - 14*k + 14011
polys = (p * q == n)
print(solve(polys, k))
#k == 13070168166947995246有了k一切好说
n = 1901485114700245088118015176838411045645808657633721129158322425051110390237801115516544893309422501851747092251796770953642000579931231478667887589988786560834446696408732292786254192492281586457284980263740183
enc = 1199361436656854951826843585559905358018072076349745598865984504434921942249797269971584270541920348511243191511578321283455075109027873358983934024677982086699270397304699932717071144314481599892879445599516848
import gmpy2
k = 13070168166947995246
p = k**6 + 7*k**4 - 40*k**3 + 12*k**2 - 114*k + 31377
q = k**5 - 8*k**4 + 19*k**3 - 313*k**2 - 14*k + 14011
d = gmpy2.invert(31337, (p-1)*(q-1))
from Crypto.Util.number import long_to_bytes
print(long_to_bytes(int(pow(enc, d, n))))
#flag{y0u_kn0w_th3_P0lyn0mialRing_w1th_RSA!!!}babyhint
1、题目信息
import gmpy2
import libnum
import uuid
from secret import flag
m=libnum.s2n(flag)
p=libnum.generate_prime(512)
q=libnum.generate_prime(512)
e=65537
n=p*q
hint1=pow(2023*p+2022*q,1919,n)
hint2=pow(2022*p+2023*q,9191,n)
c=pow(m,e,n)
print("hint1=",hint1)
print("hint2=",hint2)
print("n=",n)
print("c=",c)
'''
hint1= 83535799515204730191288403119559179388147974968301357768644756769205396635068662150926873512812305514469213626273460486537390422570056287512841114712846420160416446291128064734960979586229744062965998582728378025151822479630618024804808407804317029367335421715125562402059266983021662398390585435529976586654
hint2= 14402204438484882372730843813561914135941866642278909172674395293274736617425618184831446215507756031454895377588951726822765439585979555636320832177929472057402274116190878688601329765374509467243968967279090492272317903230101551317377700802837187081510381677262879617929177970455244249498674083943925477229
n= 94120719816617297967197808458007462810449143149204454740678593087096770130918870563878599847276923902207042790106345400843990455347835029220453217996810995363105274873857381469314548191574754245357568090646094043040797653858225598519876785530143007788084656262253002478643994943076851585839631209338814367691
c= 84244594789418833202484965138308516535996015903654462304986953156471594657993252593373963514364258027091543394305491354187806441313428473670956684437253991594327692679733432489342255718685303997647293213324463025120804679847465190496542879161344985402542539184706559207299026102682674060562738496314731555616
'''2、解题方法
题目分析:

exp
from Crypto.Util.number import *
h1= 83535799515204730191288403119559179388147974968301357768644756769205396635068662150926873512812305514469213626273460486537390422570056287512841114712846420160416446291128064734960979586229744062965998582728378025151822479630618024804808407804317029367335421715125562402059266983021662398390585435529976586654
h2= 14402204438484882372730843813561914135941866642278909172674395293274736617425618184831446215507756031454895377588951726822765439585979555636320832177929472057402274116190878688601329765374509467243968967279090492272317903230101551317377700802837187081510381677262879617929177970455244249498674083943925477229
n= 94120719816617297967197808458007462810449143149204454740678593087096770130918870563878599847276923902207042790106345400843990455347835029220453217996810995363105274873857381469314548191574754245357568090646094043040797653858225598519876785530143007788084656262253002478643994943076851585839631209338814367691
c= 84244594789418833202484965138308516535996015903654462304986953156471594657993252593373963514364258027091543394305491354187806441313428473670956684437253991594327692679733432489342255718685303997647293213324463025120804679847465190496542879161344985402542539184706559207299026102682674060562738496314731555616
e = 65537
k = 19 * 101 * 91
h5 = pow(h1,91,n)*pow(2022,k,n)-pow(h2,19,n)*pow(2023,k,n)
h6 = pow(h1,91,n)*pow(2023,k,n)-pow(h2,19,n)*pow(2022,k,n)
k1 = inverse(pow(2022,2*k,n)-pow(2023,2*k,n), n)
k2 = inverse(pow(2023,2*k,n)-pow(2022,2*k,n), n)
h3 = h5 * k1 % n
h4 = h6 * k2 % n
q = GCD(h3, n)
p = GCD(h4, n)
phi = (p-1) * (q-1)
d = inverse(e, phi)
m = pow(c,d,n)
print(bytes.fromhex(hex(m)[2:]))
#flag{ezsy_e3sy_ea4y_so_easy!!!}ezmath
1、题目信息
import libnum
from Crypto.Util.number import *
from secret import flag
m = libnum.s2n(flag)
e = 65537
p = getPrime(1024)
q = getPrime(1024)
n = p * q
c = pow(m, e, n)
hint = pow(2022 * p + 2023, q, n)
print(f'n={n}')
print(f'c={c}')
print(f'hint={hint}')
'''
n=16099847254382387482323197733210572595987701766995679577427964142162383113660616883997429365200200943640950821711084123429306946305893862414506257284441114840863787499898478803568113348661314216300658606282276936902117099898776435948501831796770856505782683585268617613575681655903107683069260253287994894440427511440504754827820494060133773435262418256886443037510658584541624614692050308222516337333585823733360631982795323752298740497235142977602602205292595197618229629610834651923388269194546316023246525302500676142502931303976146680655368617094100097945625676103639154884247373003120937959132698199043562660573
c=7980021929208497878634194663038470941705554065040985666635317762877799614984808729636911256912639929083920319066806111423231500122646366713245534616522235309310234767331344216892929739448126523171652425415458999098138841038319673380331281114806318366697490343176758140150118761408250366783210772381316729932361601257318131085116265135718477224618689710966570938280408341402386000281564650565256635313406111364916715660419153433573586809503564050585204002594864254089288672391014804368427324162776953191520483774116807593366091685560902424782104761523067998300887293902330501335485075609216897135678017158187880996872
hint=14005608544369156893681352040163362072608754453657200460825561123439158535855236943525558717120672888372079069187756549797113560863313618058077150885401191613229507892570378437310964624470055767463556516869604496669085622244233154871165554916349033197798790982409986216498996673603605465039336316170130644317728786516639634775709400754328137266154981484016505702738584209800158047120647468364899692021253904198509376650238372552486792709682170146695759196408908825447960637667502907929061819408441663880712891979320089482801220225451560809151067631824526463122992973388740015878474372614751149918455457191739542980396
'''2、解题方法
上一题的简化版。。。。
exp
from gmpy2 import *
from Crypto.Util.number import *
n=16099847254382387482323197733210572595987701766995679577427964142162383113660616883997429365200200943640950821711084123429306946305893862414506257284441114840863787499898478803568113348661314216300658606282276936902117099898776435948501831796770856505782683585268617613575681655903107683069260253287994894440427511440504754827820494060133773435262418256886443037510658584541624614692050308222516337333585823733360631982795323752298740497235142977602602205292595197618229629610834651923388269194546316023246525302500676142502931303976146680655368617094100097945625676103639154884247373003120937959132698199043562660573
c=7980021929208497878634194663038470941705554065040985666635317762877799614984808729636911256912639929083920319066806111423231500122646366713245534616522235309310234767331344216892929739448126523171652425415458999098138841038319673380331281114806318366697490343176758140150118761408250366783210772381316729932361601257318131085116265135718477224618689710966570938280408341402386000281564650565256635313406111364916715660419153433573586809503564050585204002594864254089288672391014804368427324162776953191520483774116807593366091685560902424782104761523067998300887293902330501335485075609216897135678017158187880996872
hint=14005608544369156893681352040163362072608754453657200460825561123439158535855236943525558717120672888372079069187756549797113560863313618058077150885401191613229507892570378437310964624470055767463556516869604496669085622244233154871165554916349033197798790982409986216498996673603605465039336316170130644317728786516639634775709400754328137266154981484016505702738584209800158047120647468364899692021253904198509376650238372552486792709682170146695759196408908825447960637667502907929061819408441663880712891979320089482801220225451560809151067631824526463122992973388740015878474372614751149918455457191739542980396
e = 65537
q = gcd(n,hint-pow(2023,n,n))
#print(q)
p = n//q
Fai = (p-1)*(q-1)
d = invert(e,Fai)
m = pow(c,d,n)
print(long_to_bytes(m))
#flag{ju3t_a_s1mpl3_ta3k}关键的Vigenere
1、题目信息
观其表,解其里key.txt
FNY CQ HLQSEPNVJ
提示:Keyword
(观其表,解其里)题目.txt
QGUMI{py@nessfz_tzhozr!}2、解题方法
我们的思路是这样的,看到题目说是维吉尼亚,所以肯定要key才能解,如何去找key?
看到另一个文件提示:Keyword,知道是关键字密码,我们肯定是要用这个关键字密码来解出维吉尼亚解密所需的key
但关键字密码需要知道关键字,显然没有发现。。竟然给了总会有关键字的不然没法解。
仔细读提示:观其表,解其里。。什么意思?就是观察题目外表,解附件里面密文。
所以我们发现关键字就是“Vigenere”,而且题目说关键的Vigenere,很显然。
如果实在发现不了那就把题目所涉及的所有字符都试一遍肯定有结果的。
所以我们关键字解码
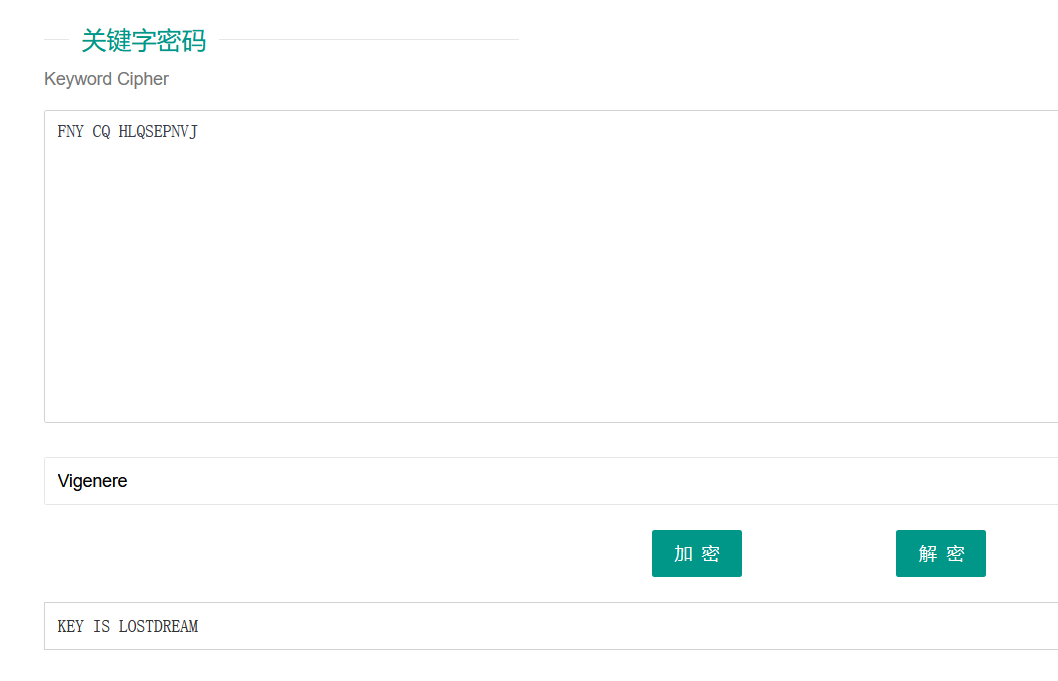
得到密匙为:
LOSTDREAM这和我们按照flag前缀手算出来的前五个字母一样,所以它就是key了,然后维吉尼亚解码

哈哈哈!!!原神启动!!!
兔帽的奇妙冒险
1、题目信息
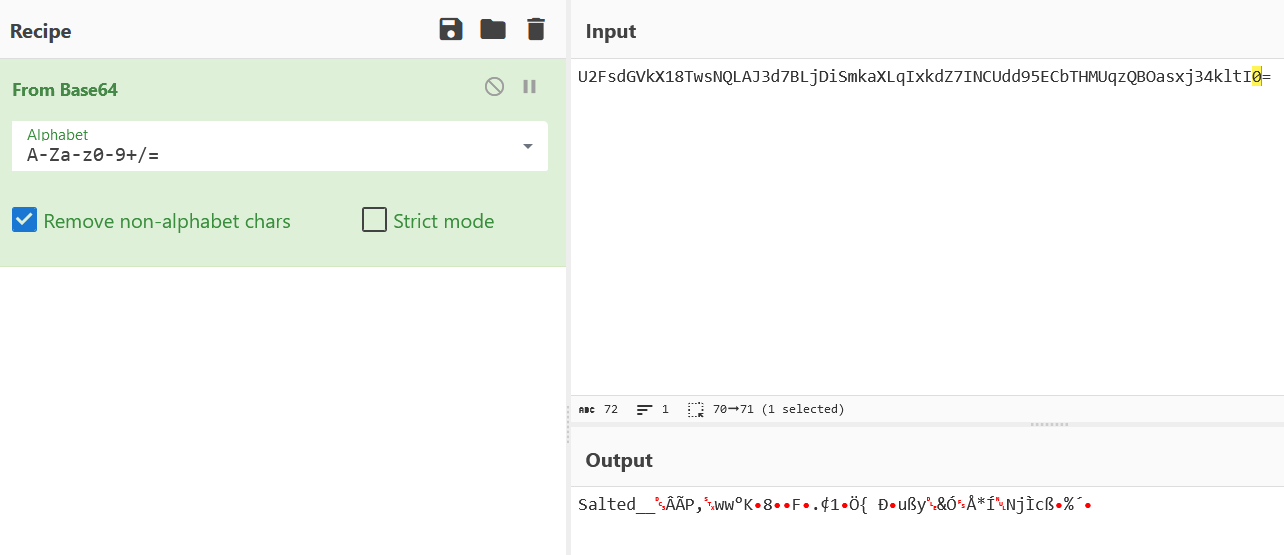
有一只名叫贝斯64先生的兔子。它戴着一顶古老的兔帽子,帽子上绣着奇异的符文,传说这是一种能与神秘力量连接的魔法帽子。
OFR3c05RTEFKM2Q3QkxqRGlTbWthWExxSXhrZFo3SU5DVWRkOTVFQ2JUSE1VcXpRQk9hc3hqMzRrbHRJMD0=2、解题方法
看到题目肯定想到要用兔子流密码解码,问题是如何获得兔子流密码?
首先,我们来分析“有一只名叫贝斯64先生的兔子。”因此可以想到是兔子流密码用base64加密了,所以我们需要base64先解一下

得到
8TwsNQLAJ3d7BLjDiSmkaXLqIxkdZ7INCUdd95ECbTHMUqzQBOasxj34kltI0=然后就是考察我们对兔子流密码的认识了,分析最后一句话“帽子上绣着奇异的符文,传说这是一种能与神秘力量连接的魔法帽子。”与神秘力量连接的魔法帽子,重点是在这个连接上。有连接说明什么?肯定是断了,哪里断了呢?我们仔细看解密后的信息发现兔子流密码一部分前缀没了,完整的兔子流密码前缀长这样
U2FsdGVkX1所以我们加上去
U2FsdGVkX18TwsNQLAJ3d7BLjDiSmkaXLqIxkdZ7INCUdd95ECbTHMUqzQBOasxj34kltI0=然后解码就OK啦

这里还有个小知识,兔子流base64后的前缀会发现是Salted开头的哈哈哈。