「代码随想录算法训练营」第五十一天 | 图论 part9
Bellman_ford算法
Bellman_ford算法解决的问题和dijkstra朴素版要解决的问题类似,唯一不同的是dijkstra解决的问题中边的权值不能为负数,而Bellman_ford算法要解决的问题是带负权值的单源最短路问题。
Bellman_ford算法的核心思想是对所有边进行松弛n-1次操作(n为节点数量),从而求得目标最短路。
松弛的概念就是当当前节点的minDist值大于从其他节点过来的权值,则更新当前节点的minDist值,如下面的代码:
if(minDist[B] > minDist[A] + value) minDist[B] = minDist[A] + value;
其中value表示从A节点到B节点中的权值,上面代码的意思就是A到B的路径所需要的权值要小于B当前的权值,因此要更新B的权值。
模拟过程
注意:这个模拟过程仅仅是将具有改变的过程展现出来,而有些节点在当前松弛阶段并没有改变其minDist值,比如节点5到节点6……,这里并没有将这些过程展现出来。
- 加入节点1,更新minDist数组。
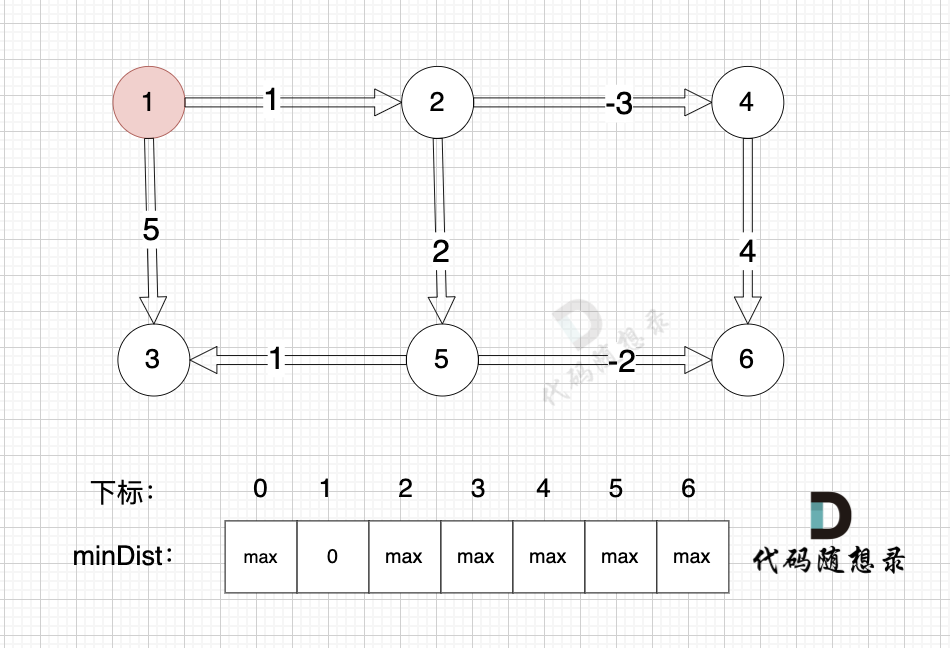
- 进行一次松弛计算:
节点1到节点2:minDist[2] > minDist[1] + 1,因此更新minDist[2]。
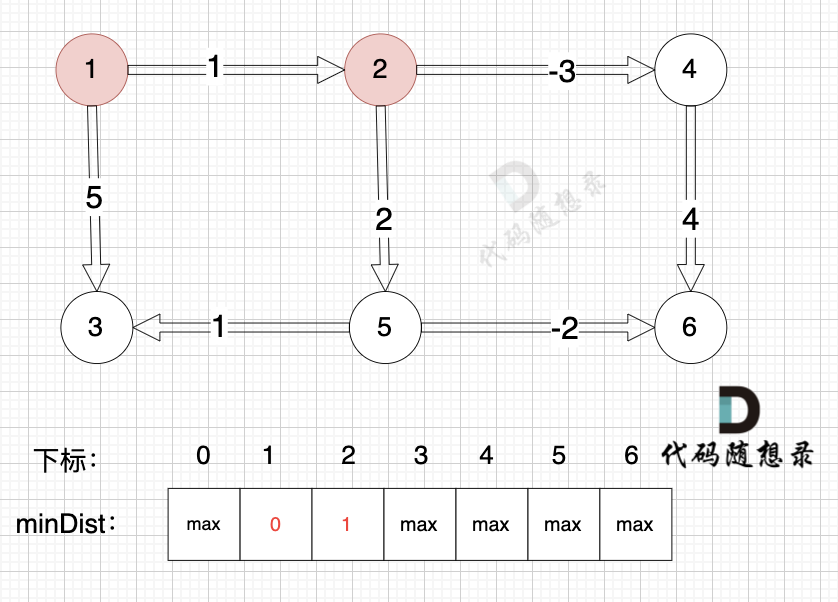
节点2到节点5:minDist[5] > minDIst[2] + 2,因此更新minDist[5]。
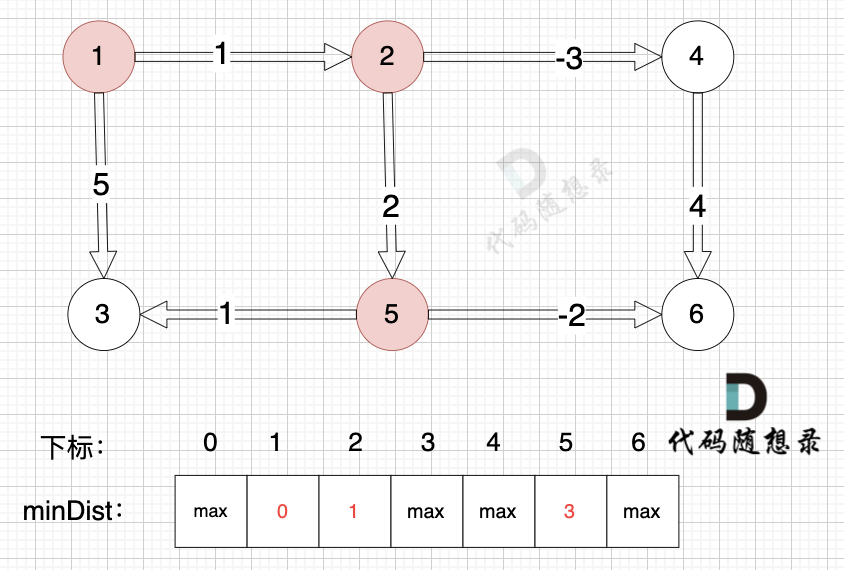
节点2到节点4:minDist[4] > minDist[2] + (-3),因此更新minDist[4]。
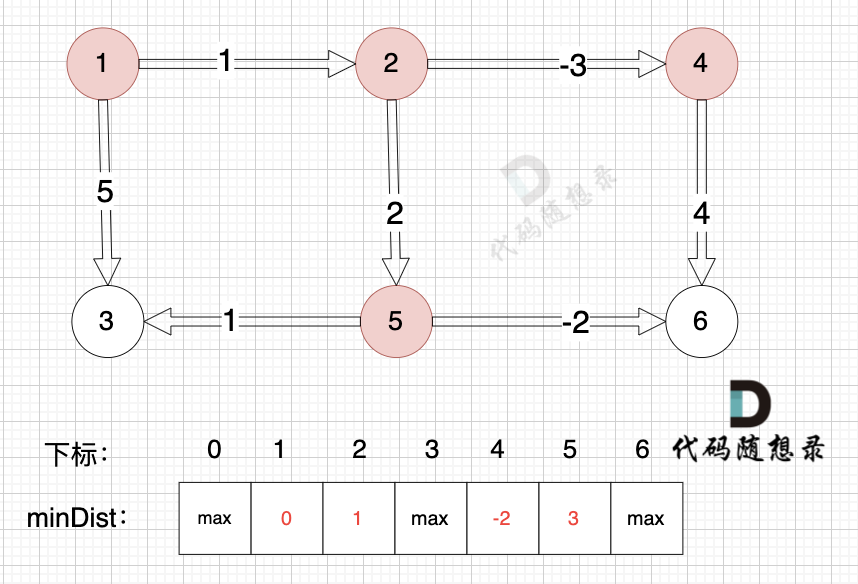
节点4到节点6:minDist[6] > minDist[4] + 4,因此更新minDist[6]。
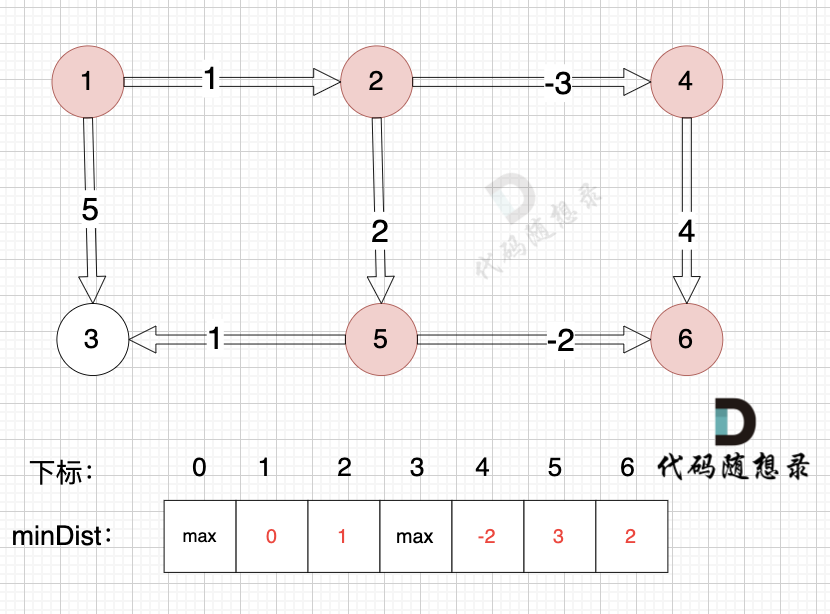
节点1到节点3:minDist[3] > minDist[1] + 5,因此更新minDist[3]。
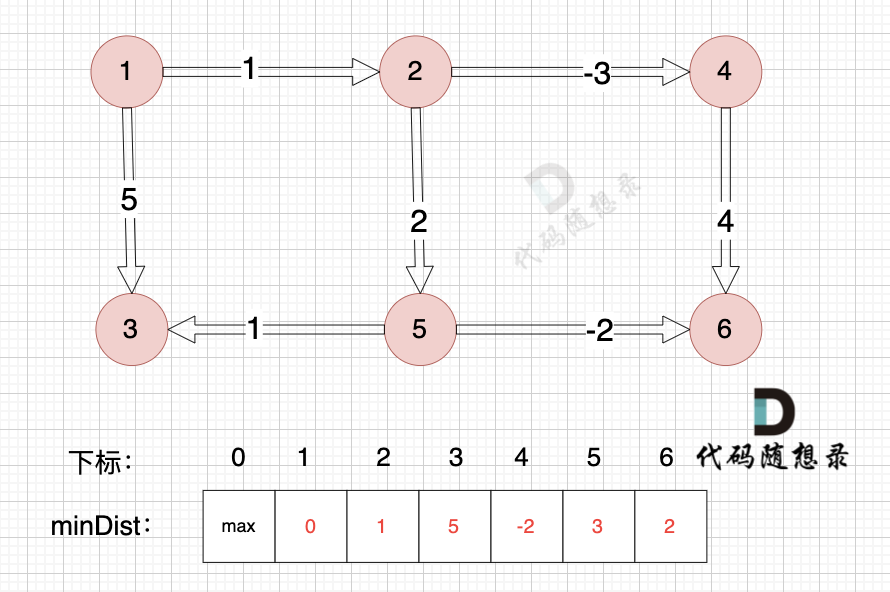
- 上面只是一次松弛的结果,相当于计算起点到达与起点一条边相连的节点的最短距离。而从起点到终点最多有n-1条边,因此需要进行n-1次松弛。
题目:94. 城市间货物运输I
题目链接:https://kamacoder.com/problempage.php?pid=1152
文章讲解:https://www.programmercarl.com/kamacoder/0094.城市间货物运输I.html
题目状态:看题解
思路:
使用Bellman_ford算法。
代码:
#include <iostream>
#include <vector>
#include <list>
#include <climits>
using namespace std;
int main()
{
int n, m, p1, p2, val;
cin >> n >> m;
vector<vector<int>> grid;
// 将所有边保存起来
for(int i = 0; i < m; ++i)
{
cin >> p1 >> p2 >> val;
grid.push_back({p1, p2, val});
}
int start = 1; // 起点
int end = n; // 终点
vector<int> minDist(n + 1, INT_MAX);
minDist[start] = 0;
// 对所有边松弛n-1次
for(int i = 1; i < n; ++i)
{
// 每一次松弛,都是对所有边进行松弛
for(vector<int> &side : grid)
{
int from = side[0]; // 边的出发点
int to = side[1]; // 边的到达点
int price = side[2]; // 边的权值
// 松弛操作
// minDist[from] != INT_MAX 防止从未计算过的节点出发
if(minDist[from] != INT_MAX && minDist[to] > minDist[from] + price)
{
minDist[to] = minDist[from] + price;
}
}
cout << "对所有边松弛" << i << "次" << endl;
for(int k = 1; k <= n; ++k)
{
cout << minDist[k] << " ";
}
cout << endl;
}
if(minDist[end] == INT_MAX) cout << "unconnected" << endl;
// 不能到达终点
else cout << minDist[end] << endl; // 到达终点最短路径
}
Bellman_ford队列优化算法(又名SPFA)
在上一节的Bellman_ford算法中的松弛阶段是对每一个节点都进行松弛,而有些节点在上一个节点没有被松弛的情况下进行松弛是没必要的。
比如当前节点5的minDist[5]为INT_MAX,而节点5到节点6需要判断minDist[6]是否大于minDist[5] + value,显然是不必要的。
而队列优化版本则只需要对上一次松弛的时候更新过的节点作为出发节点所连接的边进行松弛就够了。
模拟过程
- 将节点1压入队列,并更新minDist数组。
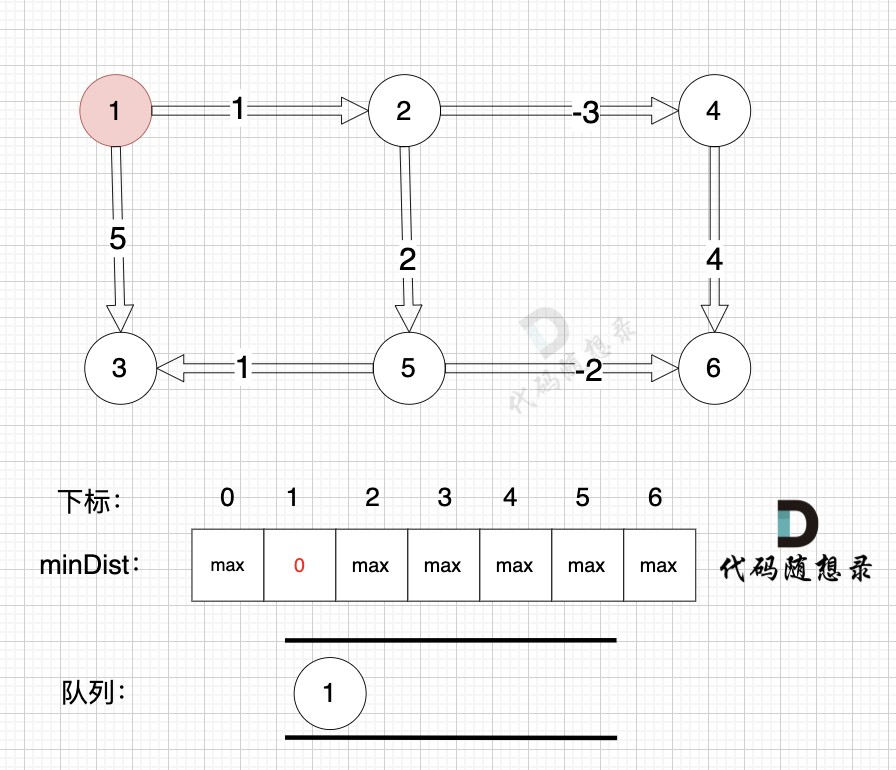
- 从队列中取出节点1,以节点1为起点,压入与其有边的节点2和节点3,并更新minDist数组。

- 从队列中取出节点2,以节点2为起点,压入与其有边的节点4和节点5,并更新minDist数组。
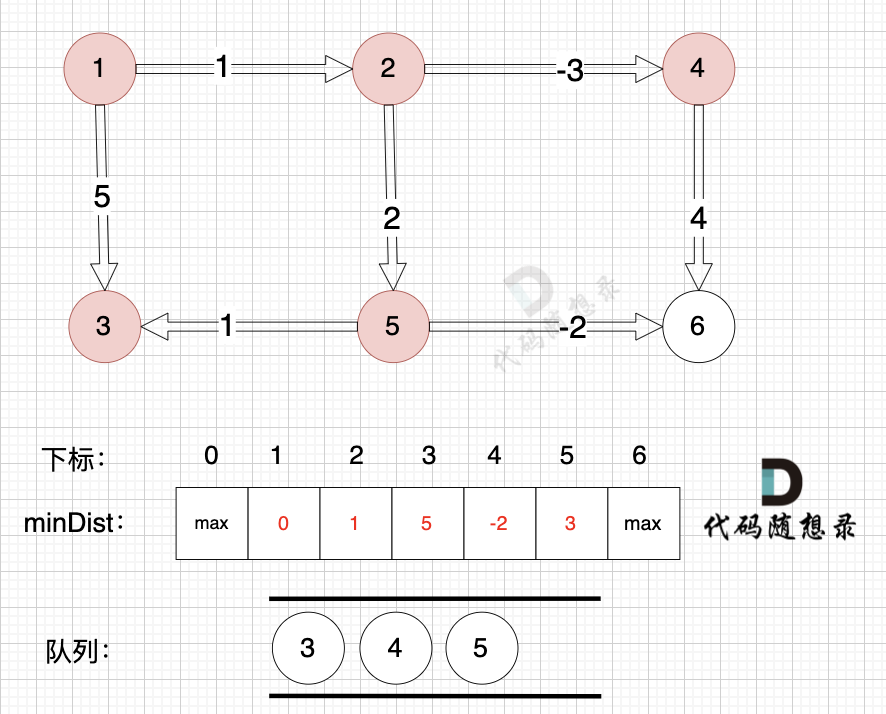
- 从队列中取出节点3,以节点3为起点,压入与其有边的节点(该例中没有),并更新minDist数组。
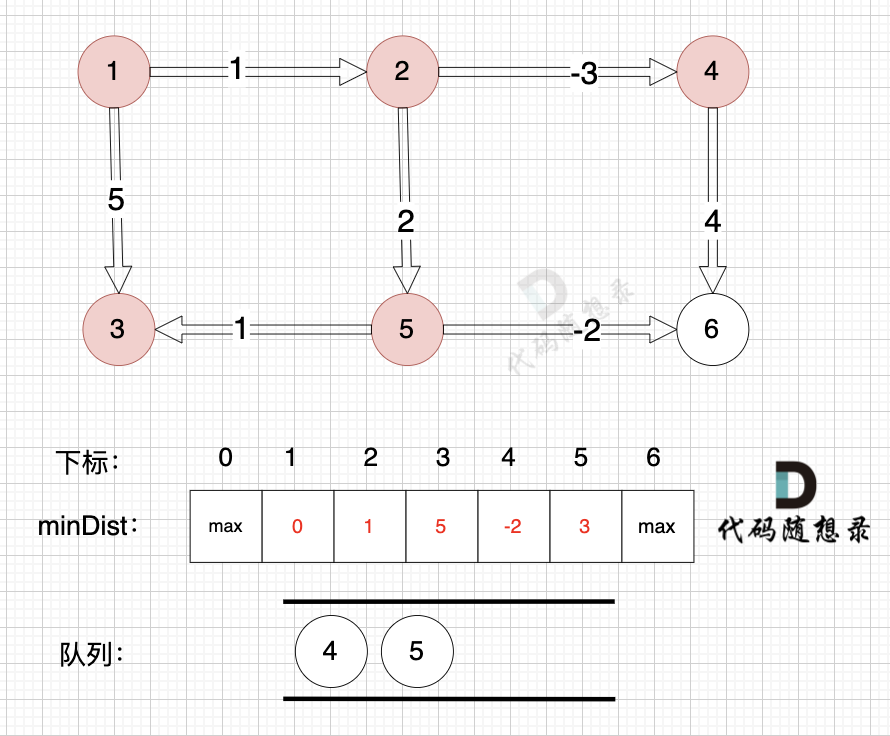
- 从队列中取出节点4,以节点4为起点,压入与其有边的节点6,并更新minDist数组。
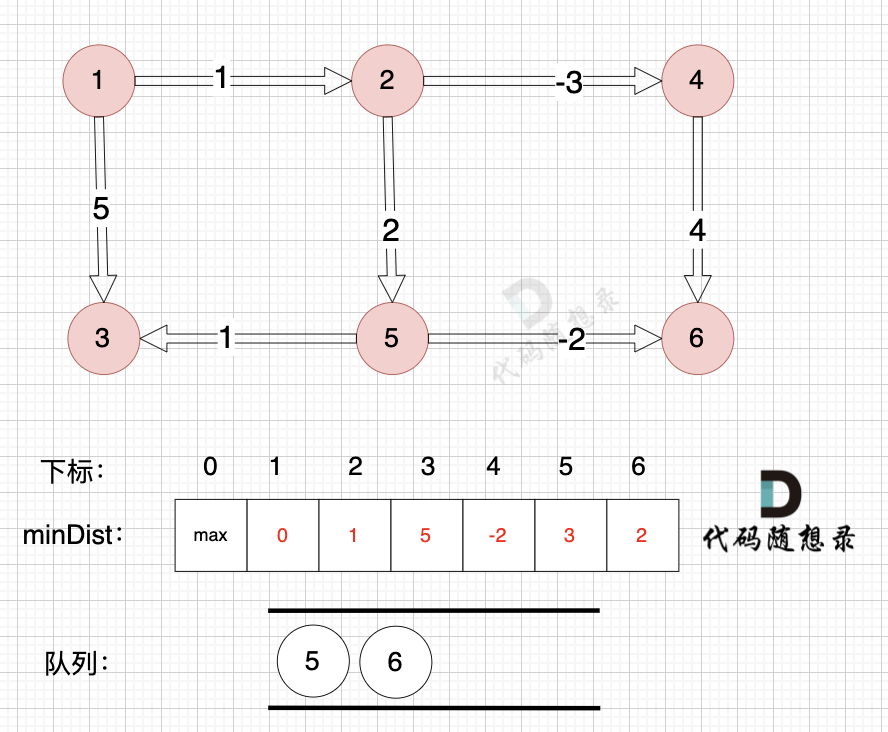
- 从队列中取出节点5,以节点5为起点,压入与其有边的节点6和节点3(因为节点6还在队列中,因此不用重复压入),并更新minDist数组。
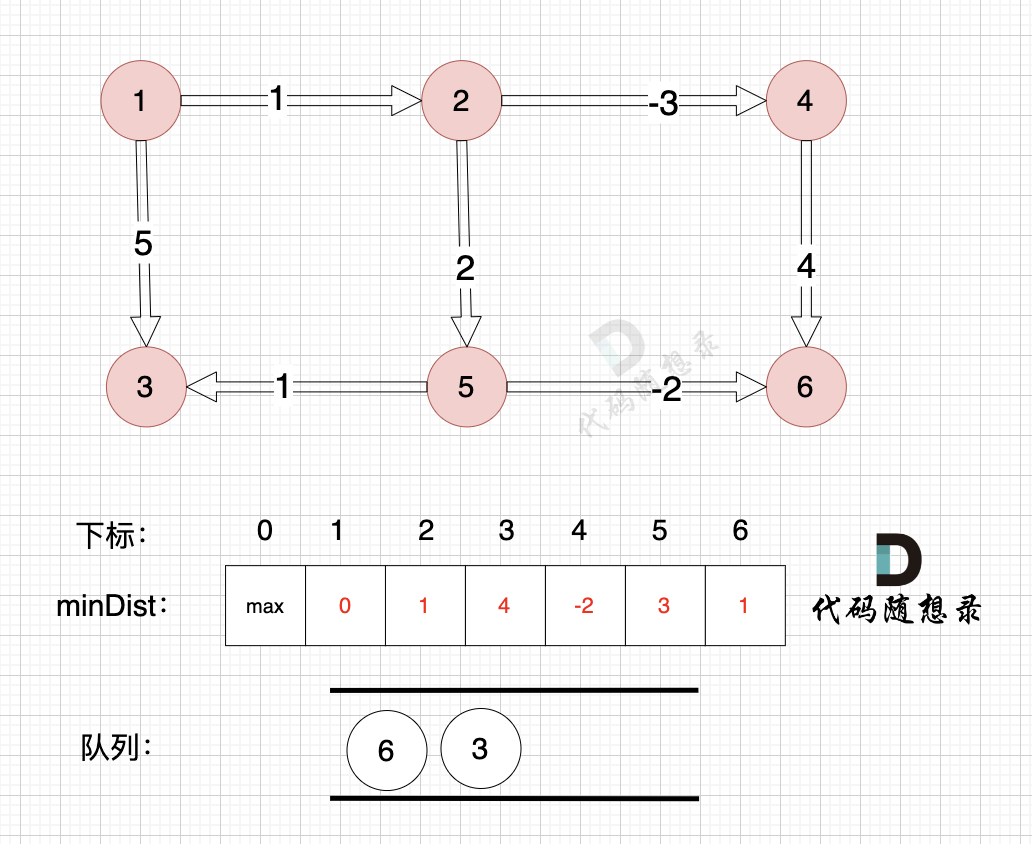
- 分别从队列中取出节点6和节点3,因为其都没有下一个节点,因此没有压入操作,而需要更新minDist数组。
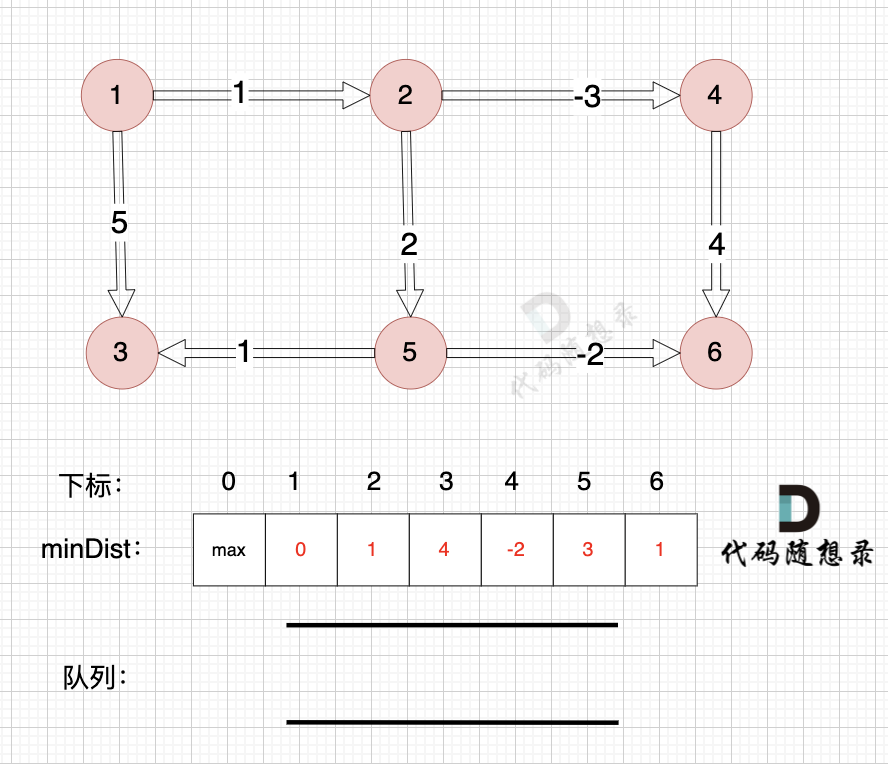
完成。
题目:94. 城市间货物运输I
题目链接:https://kamacoder.com/problempage.php?pid=1152
文章讲解:https://www.programmercarl.com/kamacoder/0094.城市间货物运输I.html
题目状态:看题解
思路:
Bellman_ford算法队列优化版本
代码:
#include <iostream>
#include <vector>
#include <queue>
#include <list>
#include <climits>
using namespace std;
// 邻接表
struct Edge
{
int to; // 链接的节点
int val; // 边的权值
Edge(int t, int w): to(t), val(w) {} // 构造函数
};
int main()
{
int n, m, p1, p2, val;
cin >> n >> m;
vector<list<Edge>> grid(n + 1);
// 加入优化,已经在队列里的元素不用重复添加
vector<bool> isInQueue(n + 1);
// 将所有边保存起来
for(int i = 0; i < m; ++i)
{
cin >> p1 >> p2 >> val;
grid[p1].push_back(Edge(p2, val));
}
int start = 1; // 起点
int end = n; // 终点
vector<int> minDist(n + 1, INT_MAX);
minDist[start] = 0;
queue<int> que;
que.push(start);
while(!que.empty())
{
int node = que.front(); que.pop();
// 从队列中取出的时候,要取消标记,我们只保证已经在队列里的元素不用重复加入
isInQueue[node] = false;
for(Edge edge : grid[node])
{
int from = node;
int to = edge.to;
int value = edge.val;
// 开始松弛
if(minDist[to] > minDist[from] + value)
{
minDist[to] = minDist[from] + value;
if(isInQueue[to] == false)
{
// 已经在队列里的元素不用重复添加
que.push(to);
isInQueue[to] = true;
}
}
}
}
// 不能到达终点
if(minDist[end] == INT_MAX) cout << "unconnected" << endl;
// 到达终点最短路径
else cout << minDist[end] << endl;
}
Bellman_ford算法之判断负权回路
上面两节都是没有回路的情况,而在本节的示例中出现了负权回路的情况,也就是说一直在这个负权回路中转到话,其minDist会一直变小,因此需要判断是否存在负权回路。
前两节都是进行n-1次松弛,因为n-1次和n次是相同的,但在本节中是不一样的,因为有负权回路的存在,n次和n-1次的结果是不同的,因此可以根据这个条件来判断是否存在负权回路。
题目:95. 城市间货物运输II
题目链接:https://kamacoder.com/problempage.php?pid=1153
文章讲解:https://www.programmercarl.com/kamacoder/0095.城市间货物运输II.html
题目状态:看题解
思路一:
在Bellman_ford算法基础上增加负权回路判断。
代码一:
#include <iostream>
#include <vector>
#include <list>
#include <climits>
using namespace std;
int main()
{
int n, m, p1, p2, val;
cin >> n >> m;
vector<vector<int>> grid;
for(int i = 0; i < m; ++i)
{
cin >> p1 >> p2 >> val;
grid.push_back({p1, p2, val});
}
int start = 1; // 起点
int end = n; // 终点
vector<int> minDist(n + 1, INT_MAX);
minDist[start] = 0;
bool flag = false;
// 松弛n次,最后一次判断负权回路
for(int i = 1; i <= n; ++i)
{
for(vector<int> &side : grid)
{
int from = side[0];
int to = side[1];
int price = side[2];
if(i < n)
{
if(minDist[from] != INT_MAX && minDist[to] > minDist[from] + price)
minDist[to] = minDist[from] + price;
}
else
{
// 多加一次松弛判断负权回路
if(minDist[from] != INT_MAX && minDist[to] > minDist[from] + price) flag = true;
}
}
}
if(flag) cout << "circle" << endl;
else if(minDist[end] == INT_MAX) cout << "unconnected" << endl;
else cout << minDist[end] << endl;
return 0;
}
思路二:
在Bellman_ford的队列优化版本中加入负权回路判断。
代码二:
#include <iostream>
#include <vector>
#include <queue>
#include <list>
#include <climits>
using namespace std;
// 邻接表
struct Edge
{
int to; // 链接的节点
int val; // 边的权重
Edge(int t, int w): to(t), val(w) {} // 构造函数
};
int main()
{
int n, m, p1, p2, val;
cin >> n >> m;
vector<list<Edge>> grid(n + 1); // 邻接表
// 将所有边保存起来
for(int i = 0; i < m; ++i)
{
cin >> p1 >> p2 >> val;
grid[p1].push_back(Edge(p2, val));
}
int start = 1; // 起点
int end = n; // 终点
vector<int> minDist(n + 1, INT_MAX);
minDist[start] = 0;
queue<int> que;
que.push(start); // 队列里放入起点
// 记录节点加入队列几次
vector<int> count(n + 1, 0);
count[start]++;
bool flag = false;
while(!que.empty())
{
int node = que.front(); que.pop();
for(Edge &edge : grid[node])
{
int from = node;
int to = edge.to;
int value = edge.val;
// 开始松弛
if(minDist[to] > minDist[from] + value)
{
minDist[to] = minDist[from] + value;
que.push(to);
count[to]++;
// 如果加入队列次数超过n-1次就说明该图有负权回路
if(count[to] == n)
{
flag = true;
while(!que.empty()) que.pop();
break;
}
}
}
}
if(flag) cout << "circle" << endl;
else if(minDist[end] == INT_MAX) cout << "unconnected" << endl;
else cout << minDist[end] << endl;
return 0;
}
Bellman_ford算法之单源有限最短路
这节是在第一节的基础上加的内容,主要是限制两个节点中间经过的节点数。
比如,题目要求最多只能经过k个节点,那么也就意味着起始位置到终止位置中间最多只能有k+1条边。
我们只需要限制Bellman_ford算法的松弛次数即可,即从第一节中的n-1变为k+1。但是要注意在每次计算minDist数组的时候要基于所有边上一次松弛的minDist数值进行计算。
题目:96. 城市间货物运输III
题目链接:https://kamacoder.com/problempage.php?pid=1154
文章讲解:https://www.programmercarl.com/kamacoder/0096.城市间货物运输III.html
题目状态:看题解
思路一:
在Bellman_ford算法的基础上修改。
代码一:
#include <iostream>
#include <vector>
#include <list>
#include <climits>
using namespace std;
int main()
{
int src, dst, k, p1, p2, val, m, n;
cin >> n >> m;
vector<vector<int>> grid;
for(int i = 0; i < m; ++i)
{
cin >> p1 >> p2 >> val;
grid.push_back({p1, p2, val});
}
cin >> src >> dst >> k;
vector<int> minDist(n + 1, INT_MAX);
minDist[src] = 0;
vector<int> minDist_copy(n + 1); // 用来记录上一次遍历的结果
for(int i = 1; i <= k + 1; ++i)
{
minDist_copy = minDist; // 获取上一次计算的结果
for(vector<int> &side : grid)
{
int from = side[0];
int to = side[1];
int price = side[2];
// 注意使用minDist_copy来计算minDist
if(minDist_copy[from] != INT_MAX && minDist[to] > minDist_copy[from] + price)
minDist[to] = minDist_copy[from] + price;
}
}
// 不能到达终点
if(minDist[dst] == INT_MAX) cout << "unreachable" << endl;
// 到达终点最短路径
else cout << minDist[dst] << endl;
}
思路二:
在Bellman_ford的队列优化版本的基础上修改。
代码二:
#include <iostream>
#include <vector>
#include <queue>
#include <list>
#include <climits>
using namespace std;
struct Edge { //邻接表
int to; // 链接的节点
int val; // 边的权重
Edge(int t, int w): to(t), val(w) {} // 构造函数
};
int main() {
int n, m, p1, p2, val;
cin >> n >> m;
vector<list<Edge>> grid(n + 1); // 邻接表
// 将所有边保存起来
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
// p1 指向 p2,权值为 val
grid[p1].push_back(Edge(p2, val));
}
int start, end, k;
cin >> start >> end >> k;
k++;
vector<int> minDist(n + 1 , INT_MAX);
vector<int> minDist_copy(n + 1); // 用来记录每一次遍历的结果
minDist[start] = 0;
queue<int> que;
que.push(start); // 队列里放入起点
int que_size;
while (k-- && !que.empty()) {
minDist_copy = minDist; // 获取上一次计算的结果
que_size = que.size(); // 记录上次入队列的节点个数
while (que_size--) { // 上一轮松弛入队列的节点,这次对应的边都要做松弛
int node = que.front(); que.pop();
for (Edge edge : grid[node]) {
int from = node;
int to = edge.to;
int price = edge.val;
if (minDist[to] > minDist_copy[from] + price) {
minDist[to] = minDist_copy[from] + price;
que.push(to);
}
}
}
}
if (minDist[end] == INT_MAX) cout << "unreachable" << endl;
else cout << minDist[end] << endl;
}