太阳对月球的引力比地球大两倍多,为什么月球会一直跟着地球跑?
月球在太阳系中主要会受到两个天体的引力,一个是地球,另一个是太阳,通常来讲,有不少人都会认为地球对月球的引力比太阳大,所以月球才会一直跟着地球跑,而没有被太阳吸过去,但我们仔细计算一下就会发现事实并不是这样的。

已知太阳、地球和月球的质量分别为1.989 x 10^30千克、5.965 x 10^24千克、7.349 x 10^22千克,太阳和月球平均距离为1.496 x 10^11米,地球和月球平均距离为3.844 x 10^8米。
我们将上述数据代入牛顿给出的万有引力计算公式“F = GMm/r^2”,再将其中的引力常量取值为6.67 x 10^(-11),就可以计算出太阳对月球的引力约为4.36 x 10^20牛顿,而地球对月球的引力则约为1.99 x 10^20牛顿,可以看到,太阳对月球的引力比地球大两倍多。

那么问题就来了,既然太阳对月球的引力比地球更大,那为什么月球会一直跟着地球跑,而没有被太阳吸过去?
其实月球的运动可以简单地描述为:月球一直在与地球一起围绕着太阳做圆周运动,在此过程中,太阳对月球和地球的引力充当了向心力,另一方面,月球又一直在围绕着地球做圆周运动,在此过程中,地球对月球的引力充当了向心力,其运行轨迹大概是下图这样的。
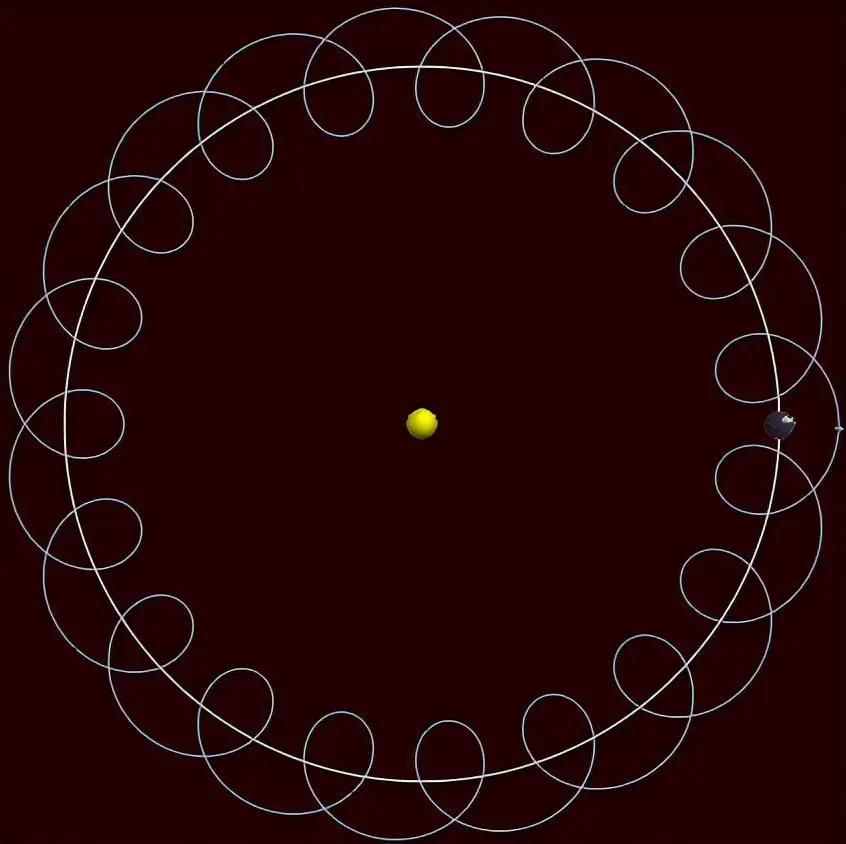
(注:上图是为了方便大家理解月球的运行轨迹,实际情况并没有这么夸张)
由此可见,对于月球来讲,太阳引力和地球引力并不是像在拔河一样,而是形成了一种持久且稳定的平衡,这样就可以让月球一直处于“在围绕着太阳公转的同时,又一直跟着地球跑”这种状态。
为什么会形成这种平衡呢?这就要说到“限制性三体问题”,这是三体问题的一种特殊情况,简单来讲就是:在三个天体中,有一个天体的质量相对于其他两个天体很小,以至于可以忽略。
“限制性三体问题”有五个名为“拉格朗日点”的特解,一般将它们分别称为“L1、L2、L3、L4、L5”,我们可以简单理解为,“拉格朗日点”是“限制性三体问题”中的两个质量较大的天体的引力平衡点,假如质量最小的那个天体位于“拉格朗日点”,那么它就可以与质量第二大的天体保持同步运动。

上图为太阳与地球的五个“拉格朗日点”,其中“L1”和“L2”都位于地球附近,它们与地球的距离均为150万公里,位于这两个位置的小天体刚好可以与地球同步围绕太阳公转,这也就意味着,在“L1”和“L2”的位置上,地球的引力可以保证小天体不会远离自己而去。
由于引力的大小与距离的平方是反比例关系,如果一个小天体比“L1”和“L2”离地球更近,那么地球对它的引力就会更大,这个小天体就更不会远离地球了。
反过来讲,如果一个小天体比“L1”和“L2”离地球更远,那么地球对它的引力就会减小,以至于无法使其与自己保持同步,因此这个小天体就离地球越来越远(至于它会不会被太阳吸过去,则要看它的运动方向以及相对于太阳的速度)。
所以我们可以得出一个结论:在以地球为中心,半径为150万公里(即“L1”和“L2”与地球的距离)的球体空间内,地球的引力可以保证小天体不会远离,也就是说,只要月球一直运行在这个球体空间之内,它就不会远离地球而去。

事实上,月球与地球的距离最远也只有40.5万公里,远远小于上述球体空间的半径,在此基础上,再加上月球刚好拥有合适的运动方向以及相对于地球的速度,所以它就能稳定地围绕着地球公转,从而实现“在围绕着太阳公转的同时,又一直跟着地球跑”。