【scipy 基础】--积分和微分方程
对于手工计算来说,积分计算是非常困难的,对于一些简单的函数,我们可以直接通过已知的积分公式来求解,但在更多的情况下,原函数并没有简单的表达式,因此确定积分的反函数变得非常困难。
另外,相对于微分运算来说,积分运算则具有更多的多样性,包括不同的积分方法(如换元积分法、分部积分法等)和积分技巧,需要根据具体的函数形式选择合适的方法,这增加了积分运算的复杂性。
而微分运算有一条基本的规则,即导数运算具有线性性质,可以通过求导法则来简化计算。
Scipy库的积分子模块为我们提供了便捷的积分和微分方程计算接口。
利用Scipy,进行数学或科学研究时,可以把更多的时间花在原理和推导上,计算过程交由Scipy去处理。
1. 主要功能
Scipy的积分模块主要用于进行数学方程的求解和过程控制。
该模块提供了一组函数,可以用于求解一元和多元函数的导数、积分、二阶导数和偏导数等。
此外,该模块还提供了一些用于过程控制和优化的函数。
此模块的函数主要分为以下几类:
- 针对函数对象的积分
- 针对固定样本的积分
- 常微分方程
总之,scipy.integrate模块提供了丰富的函数和算法,用于解决各种数学问题和过程控制问题。
下面通过一些示例来了解其使用方法。
2. 积分运算
2.1. 一重积分
比如计算曲线 \(y = e^{-x}\)在 \(-0.75 \leqslant x \leqslant 0.5\)范围内的面积。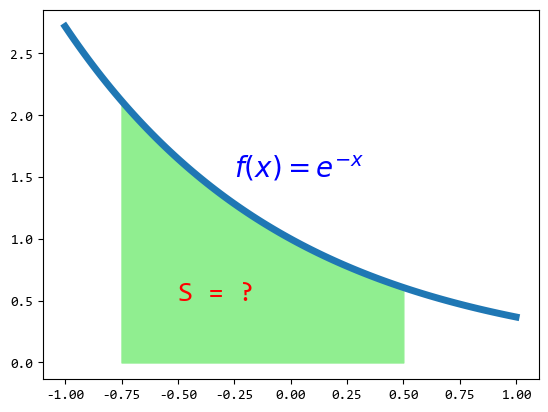
也就是计算积分:\(\int_{-0.75}^{0.5}e^{-x}dx\)
from scipy.integrate import quad
y = lambda x: np.exp(-x)
integral, integral_err = quad(y, -0.75, 0.5)
print("面积为:{}".format(integral))
# 运行结果
面积为:1.5104693569000414
2.2. 二重积分
所谓二重积分,就是积分变量有两个,依次在两个变量上积分得出最终的结果。
比如,对于函数:\(z = x^2 + y^2\),相当于如下的三维曲面。
计算上面的曲面在 \(-2 \leqslant x \leqslant 2\)且 \(-1 \leqslant y \leqslant 1\)情况下,与XY平面所包围的体积。
即:\(\int_{-2}^2\int_{-1}^1(x^2+y^2)dydx\)
from scipy.integrate import dblquad
integrand = lambda y, x: x**2 + y**2
integral, integral_error = dblquad(integrand, -2, 2, -1, 1)
print("体积为:{}".format(integral))
# 运行结果
体积为:13.333333333333334
这个示例中的曲面在X平面和Y平面上是对称的,计算二重积分时,先积分x,还是先积分y,结果是一样的。
也就是:\(\int_{-2}^2\int_{-1}^1(x^2+y^2)dydx = \int_{-2}^2\int_{-1}^1(x^2+y^2)dxdy\)
其他的曲面不一定是对称的,所以二重积分时一定要注意积分的顺序。
3. 常微分方程求解
常微分方程是一类以未知函数和其导数为主要研究对象的数学方程,适合描述不断变化的场景。
3.1. 一元常微分方程
比如计算物体速度的时候,如果加速度恒定,根据牛顿运动定律,很容易就能计算出速度和时间的关系。
但是若加速度也会不断变化的话,如何确定速度和时间的关系呢?
比如假设加速度随速度和时间变化的关系是: \(a = v+3t\)
因为加速度也可以表示为:\(a = \frac{dv}{dt}\),也就是速度对时间的微分,即:\(a = v'\)。
这样,就得到:\(a = \frac{dv}{dt} = v' = v+3t\),其中,\(v' = v+3t\)就是一个常微分方程。
假设时间t为0时,速度v也为0,则得到:\(v'-v-3t=0, v(0)=0\)
下面利用Scipy来求解这个一元常微分方程。
from scipy.integrate import odeint
# v是速度,t是时间
def dvdt(v, t):
return v + 3*t
v0 = 0
t = np.linspace(0, 1, 100)
# 结果res是 N行1列的二维数组(因为是一元方程)
res = odeint(dvdt, v0, t)
# 转置之后第一行就是各个时间点的速度
res_v = res.T[0]
# 绘制速度和时间的关系
plt.plot(t, res_v)
plt.show()
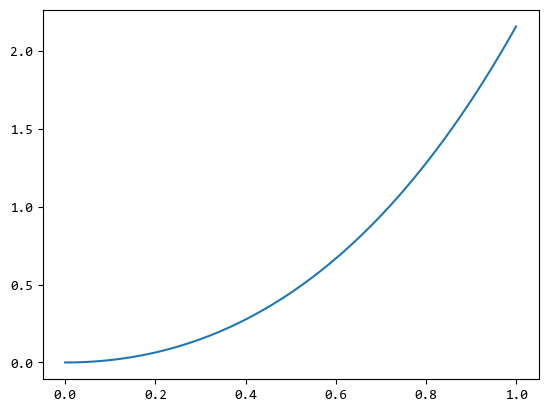
图中曲线的斜率就是加速度,可以看出加速度是随时间不断变大的。
3.2. 二元常微分方程组
对于二元常微分方程组,同样也可以用 scipy 来求解。
比如如下方程组:
\(\begin{align*}
& y_1' = y_1 + y_2^2 - 5x \quad & y_1(0)=0\\
& y_2' = 2y_1 + y_2^3 + sin(x) \quad & y_2(0)=0
\end{align*}\)
求解方法:
from scipy.integrate import odeint
# 创建方程组
def dSdx(S, x):
y1, y2 = S
return [
y1 + y2**2 - 5 * x,
2 * y1 + y2**3 + np.sin(x),
]
# 方程组初始值
y1_0 = 0
y2_0 = 0
S_0 = (y1_0, y2_0)
x = np.linspace(0, 1, 100)
sol = odeint(dSdx, S_0, x)
y1_sol = sol.T[0]
y2_sol = sol.T[1]
# 分别绘制y1,y2和x的关系
plt.plot(x, y1_sol, label="y1")
plt.plot(x, y2_sol, label="y2")
plt.legend()
plt.show()

4. 总结
积分和常微分方程算是应用非常广,但手工计算非常麻烦的两种数学工具,
在学校学习高等数学的时候应该没少吃过这两种计算的苦。
有了Scipy的帮助,则可以摆脱这类复杂计算带来的痛苦,让我们可以专注于创建解决问题的方程。