非极大值抑制(NMS)算法详解
NMS(non maximum suppression)即非极大值抑制,广泛应用于传统的特征提取和深度学习的目标检测算法中。
NMS原理是通过筛选出局部极大值得到最优解。
在2维边缘提取中体现在提取边缘轮廓后将一些梯度方向变化率较小的点筛选掉,避免造成干扰。
在三维关键点检测中也起到重要作用,筛选掉特征中非局部极值。
在目标检测方面,无论是One-stage的SSD系列算法、YOLO系列算法还是Two-stage的基于RCNN系列的算法,非极大值抑制都是其中必不可少的一个组件,可以将较小分数的输出框过滤掉,同样,在三维基于点云的目标检测模型中亦有使用。
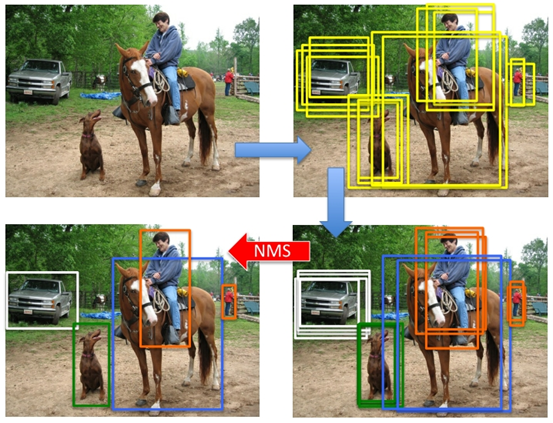
在现有的基于anchor的目标检测算法中,都会产生数量巨大的候选矩形框,这些矩形框有很多是指向同一目标,因此就存在大量冗余的候选矩形框。非极大值抑制算法的目的正在于此,它可以消除多余的框,找到最佳的物体检测位置。
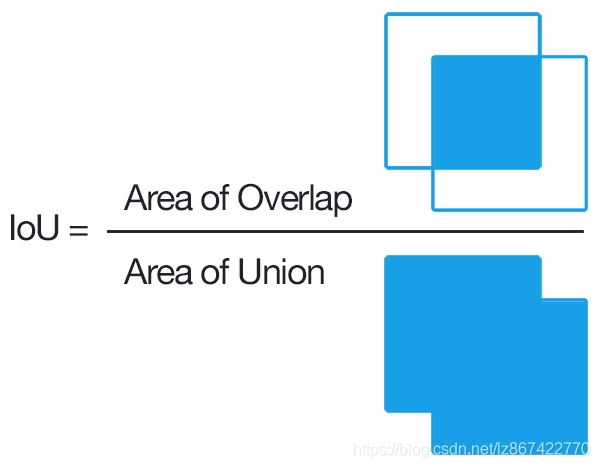
IoU(Intersection over Union) :定位精度评价公式。
相当于两个区域交叉的部分除以两个区域的并集部分得出的结果。
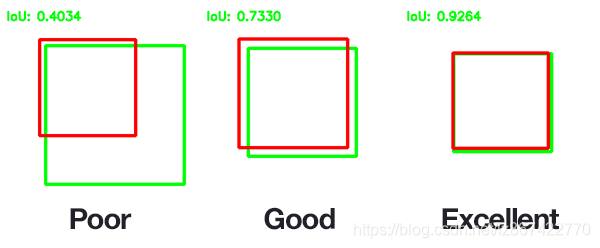
IoU各个取值时的情况展示,一般来说,这个 Score > 0.5 就可以被认为一个不错的结果了。
IOU计算:
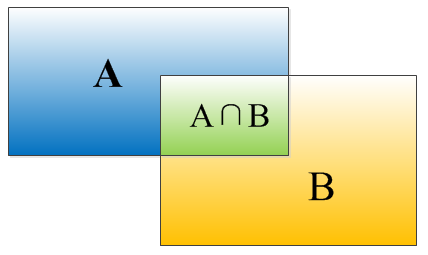
如何计算IoU(交并比)

选取两个矩形框左顶角的横,纵坐标的最大值,x21,y21;选取两个矩形框右下边角的横纵坐标的最小值,x12,y12;
- 交集面积计算:
\[{Area(A \cap B)} = |x12 - x21| * |y12 - y21|
\]
- 并集面积计算:
\[{Area(A \cup B)} = |x11 - x12| * |y11 - y12| + |x21 - x22| * |y21 - y22| - {Area(A \cap B)}
\]
- 计算IOU公式
\[IoU = \frac {Area(A \cap B)} {Area(A \cup B)}
\]
算法流程如下:
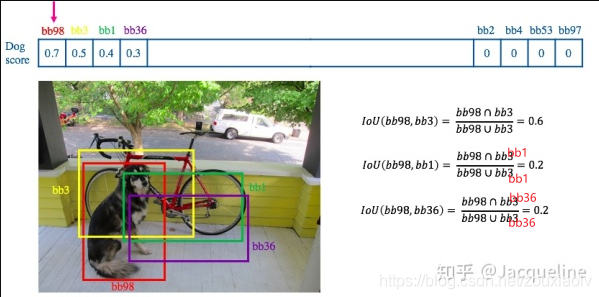
- 将所有框的得分排序,选中最高分及其对应的框
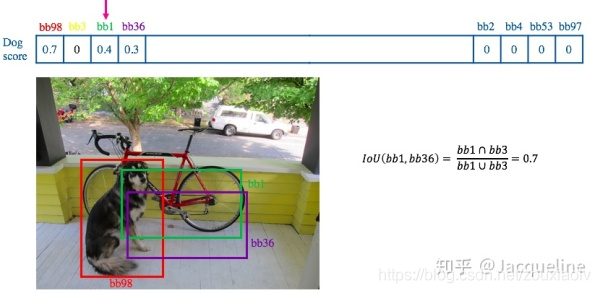
- 遍历其余的框,如果和当前最高分框的重叠面积(IOU)大于一定阈值(常用的值为0.5左右),我们就将框删除。(为什么要删除,是因为超过设定阈值,认为两个框的里面的物体属于同一个类别,比如都属于狗这个类别。我们只需要留下一个类别的可能性框图即可。)
- 从未处理的框中继续选一个得分最高的,重复上述过程。

代码如下:
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
NMS function(Non-Maximum Suppression, 抑制不是极大值的元素)
psedocode:
1. choose the highest score element a_1 in set B, add a_1 to the keep set C
2. compute the IOU between the chosen element(such as a_1) and others elements in set B
3. only keep the nums at set B whose IOU value is less than thresholds (can be set as >=0.5), delete the nums similiar
to a_1(the higher IOU it is , the more interseciton between a_1 and it will have)
4. choose the highest score value a_2 left at set B and add a_2 to set C
5. repeat the 2-4 until there is nothing in set B, while set C is the NMS value set
"""
import numpy as np
# boxes表示人脸框的xywh4点坐标+相关置信度
boxes = np.array([[100, 100, 210, 210, 0.72],
[250, 250, 420, 420, 0.8],
[220, 220, 320, 330, 0.92],
[230, 240, 325, 330, 0.81],
[220, 230, 315, 340, 0.9]])
def py_cpu_nms(dets, thresh):
# dets:(m,5) thresh:scaler
x1 = dets[:, 0] # [100. 250. 220. 230. 220.]
y1 = dets[:, 1] # [100. 250. 220. 240. 230.]
x2 = dets[:, 2] # [210. 420. 320. 325. 315.]
y2 = dets[:, 3] # [210. 420. 330. 330. 340.]
areas = (y2 - y1 + 1) * (x2 - x1 + 1)
scores = dets[:, 4] # [0 1 3 4 2]
keep = []
# index表示按照scores从高到底的相关box的序列号
index = scores.argsort()[::-1] # [2 4 3 1 0]
while index.size > 0:
print("sorted index of boxes according to scores", index)
# 选择得分最高的score直接加入keep列表中
i = index[0]
keep.append(i)
# 计算score最高的box和其他box分别的相关交集坐标
x11 = np.maximum(x1[i], x1[index[1:]]) # [220. 230. 250. 220.] 最高的被提走了,所以要从1开始取后 4位
y11 = np.maximum(y1[i], y1[index[1:]]) # [230. 240. 250. 220.]
x22 = np.minimum(x2[i], x2[index[1:]]) # [315. 320. 320. 210.]
y22 = np.minimum(y2[i], y2[index[1:]]) # [330. 330. 330. 210.]
print("x1 values by original order:", x1)
print("x1 value by scores:", x1[index[:]]) # [220. 220. 230. 250. 100.]
print("x11 value means replacing the less value compared" \
" with the value by the largest score :", x11)
# 计算交集面积
w = np.maximum(0, x22 - x11 + 1) # the weights of overlap
h = np.maximum(0, y22 - y11 + 1) # the height of overlap
overlaps = w * h
# 计算相关IOU值(交集面积/并集面积,表示边框重合程度,越大表示越相似,越该删除)
# 重叠面积 /(面积1+面积2-重叠面积)
ious = overlaps / (areas[i] + areas[index[1:]] - overlaps)
# 只保留iou小于阈值的索引号,重复上步
idx = np.where(ious <= thresh)[0]
# 因为第一步index[0]已经被划走,所以需要原来的索引号需要多加一
index = index[idx + 1]
return keep
import matplotlib.pyplot as plt
def plot_bbox(ax, dets, c='b', title_name="title"):
x1 = dets[:, 0]
y1 = dets[:, 1]
x2 = dets[:, 2]
y2 = dets[:, 3]
ax.plot([x1, x2], [y1, y1], c)
ax.plot([x1, x1], [y1, y2], c)
ax.plot([x1, x2], [y2, y2], c)
ax.plot([x2, x2], [y1, y2], c)
ax.set_title(title_name)
if __name__ == '__main__':
# 1.创建画板fig
fig = plt.figure(figsize=(12, 6))
# 参数解释,前两个参数 1,2 表示创建了一个一行两列的框 第三个参数表示当前所在的框
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)
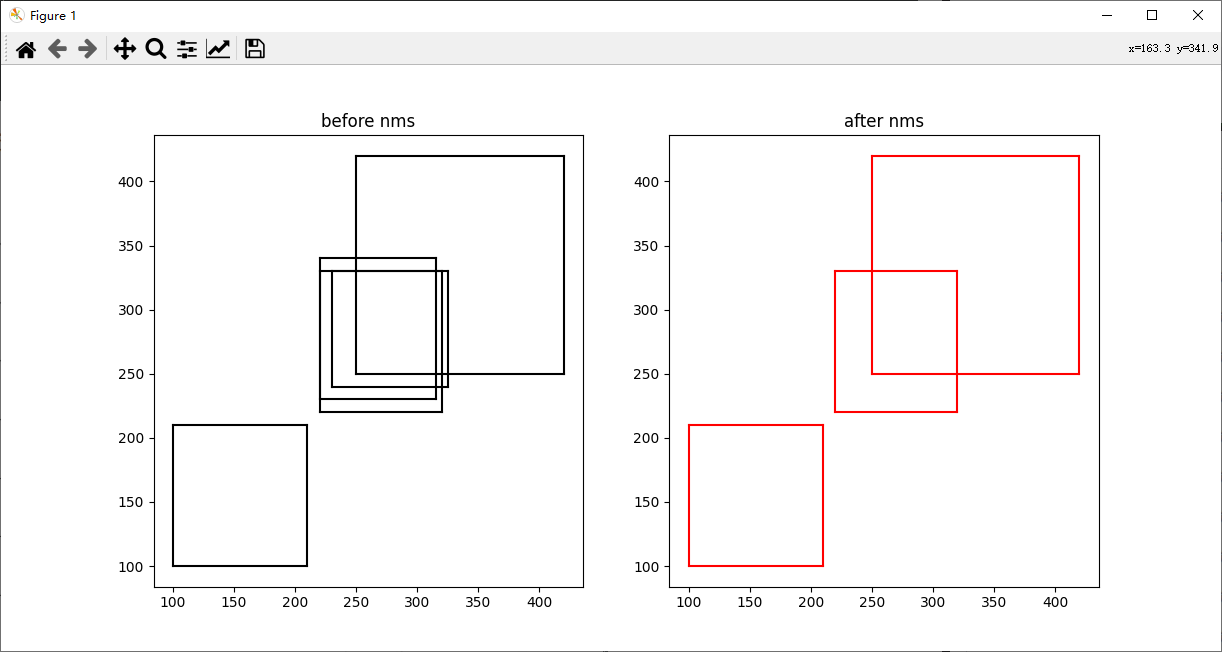
plot_bbox(ax1, boxes, 'k', title_name="before nms") # before nms
keep = py_cpu_nms(boxes, thresh=0.7)
plot_bbox(ax2, boxes[keep], 'r', title_name="after nms") # after nms
plt.show()
参考文献:
https://blog.csdn.net/weixin_42237113/article/details/105743296
https://blog.csdn.net/lz867422770/article/details/100019587