T2
题目描述
给你下列7种形状,问恰好填满 \(n*2\) 的方格有多少种方案(每种形状可任意旋转)
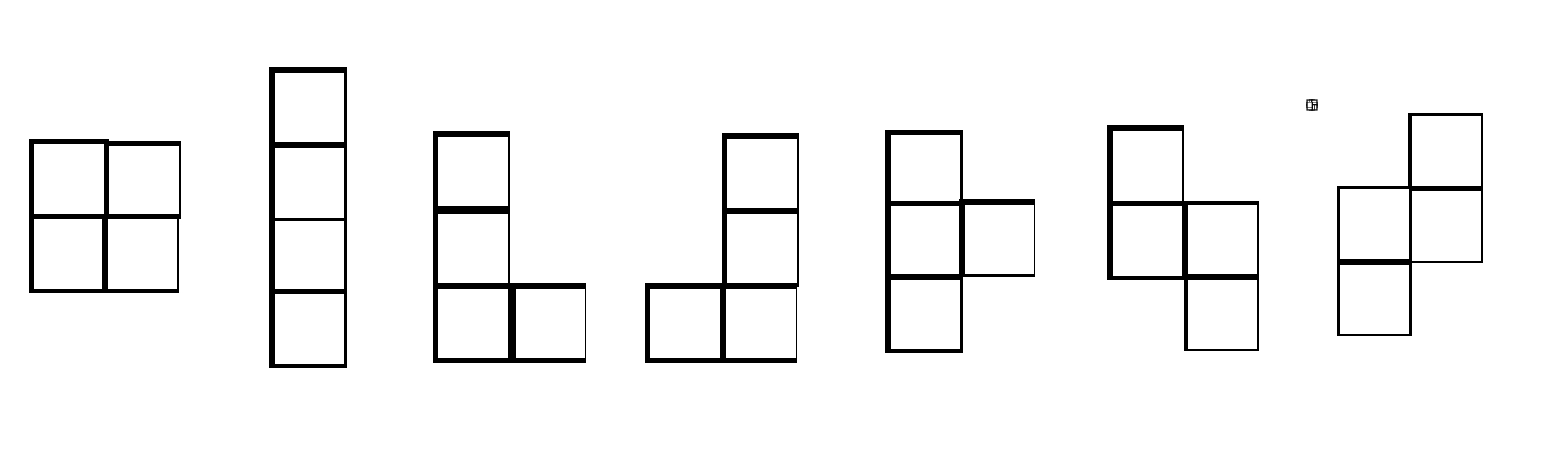
后三种形状纯粹是出题人的恶意,d用没有
做法一:暴力
不会
做法二:递推
定义:
- f[i] 为填满 \(i*2\) 的方格的方案数
- g[i] 为填满 \(i*2\) 的方格 不能被腰斩 的方案数
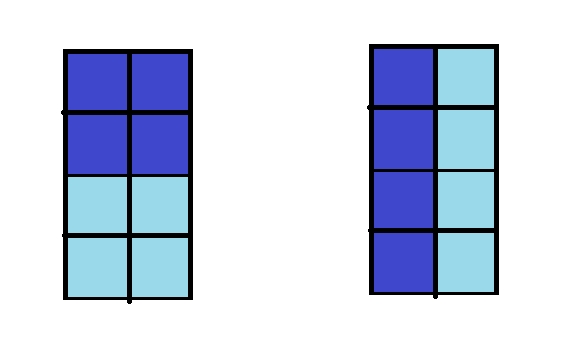
解释:例如当 \(n = 4\) 时,下列第一种画法能被腰斩,第二种不能
初步分析
很容易得到, 当 \(i\) 为奇数时 答案答案显然为0
且
\[f[0] = 1, g[0] = 1, f[2] = 1, g[2] = 1, f[4] = 4, g[4] = 3
\]
当i为大于4的偶数时
\[f[i] = g[i] * f[0] + g[i - 2] * f[2] + g[i - 4] * f[4] + ... + g[2] * f[i - 2]
\]
进一步发现
\[g[i] = 2
\]
解释:上下两端用第3, 第4种方块, 中间用2填满
然后可以得到递推式
\[f[i] = 2 * (f[0] + f[2] + f[4] + ... f[i - 6]) + 3 * f[i - 4] + f[i - 2]
\]
前面一部分可用前缀和优化一下变为:
\[f[i] = 2 * (sum[i - 6]) + 3 * f[i - 4] + f[i - 2]
\]
发现奇数项根本没有用,优化一下空间
\[f[i] = 2 * (sum[i - 3]) + 3 * f[i - 2] + f[i - 1]
\]
此时答案为 \(f[\dfrac{n}{2}]\)
进一步优化
\(O(n)\) 做法跑 \(10^{18}\) 肯定会爆,考虑上述式子用矩阵乘法优化
\[\left[ \begin{matrix}
f[i] \\
f[i - 1] \\
sum[i - 2]
\end{matrix}
\right] = \left[
\begin{matrix}
1 & 3 & 2\\
1 & 0 & 0\\
0 & 1 & 1
\end{matrix}
\right] \left[
\begin{matrix}
f[i - 1] \\
f[i - 2] \\
sum[i - 3]
\end{matrix}
\right] \]
至此,复杂度优化为\(O(nlogn)\)
其他做法
机房大佬说这题就时斐波那契第n项的平方
我太弱了不会推